통계 이론은 이미 알고 있는 약간의 정보를 이용하여 미지의 상황을 파악하는데 도움을 주는 과학적인 방법이다. 미지의 상황이란 항상 확정적 사건이라기보다는 어떤 사건이 더 발생할 가능성이 많은가로 평가되어야 함은 당연하다.
그래서 확률의 개념은 매우 빈번하게 사용되고 있다.
그러나 정확한 확률을 계산한다는 것은 매우 지루하고 힘든 과정을 요한다.
그래서 어떤 사건이 일어날 수 있는 가능성을 표로 요약한 것을 확률분포라고 한다.
이러한 확률분포를 만들기 위해서는 각 사건이 일어날 가능성을 찾아야 하는데, 때론 이 과정이 매우 어렵다.
다행히 어떤 사건이 규칙성이 있어 수학적 함수로 표현 가능하다면 확률의 계산은 매우 편리할 것이며, 더욱이 이 수학적 함수가 우리 실생활에서 흔히 일어날 수 있는 사건과 유사하다면 매우 유용할 것이다. 이러한 유용한 함수를 확률분포 함수라 하며 정규분포, 이항 분포, 카이제곱 분포, t-분포, F-분포 등이 이미 유용하게 사용하고 있는 분포는 다양하다.
📕표본 분포
표본을 이용하기 때문에 발생하는 것으로 표본 통계량의 분포를 지칭한다. 표본을 뽑게 되면 뽑힌 자료를 이용하여 통계량을 계산할 수 있으나, 이 통계량의 값은 표본이 어떻게 뽑히느냐에 따라 달라질 것이다. 그래서 통계량은 확률변수가 되며 통계 이론에 의해 일정한 분포 함수를 갖게 된다.
📕모집단 분포의 추론
모집단에서 임의로 뽑은 표본(random sample)들의 분포가 모집단의 분포와 항상 비슷하게 나온다는 보장이 없다. 특히 표본이 개수가 적은 경우 표본의 분포로 모집단의 형태를 추론하기는 어렵다.
📕모수의 추론
모집단에서 실제로 관심을 갖는 것은 분포의 형태보다는 모수의 값이다. 모수를 추론하기 위하여 표본들을 적당한 형태로 변환한 표본들의 함수인 통계량(예를 들어 표본 평균, 표본 분산 등)을 구하게 된다. 그런데 이러한 통계량 값은 우리가 얻은 표본에 따라 매번 다른 값이 나올 것이다. 즉 통계량은 확률변수이며, 어떤 확률 분포를 따르게 된다.
📕통계량의 확률분포
표본을 이용하여 구한 통계량이 모수에 얼마나 근접한 값일까? 하는 의문은 당연히 발생한다. 왜냐하면 모수와 멀어져 있는 통계량은 가치가 없으며 그래서 대부분의 사람들은 통계량을 모수와 가까운 값으로 찾기를 원한다. 그래서 구한 통계량이 모수와 얼마나 다를까 혹은 같을까를 판단할 수 있는 방법이 필요하다.
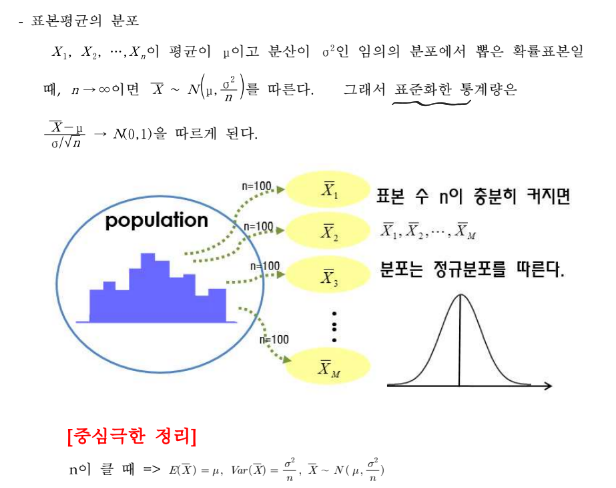
📕중심 극한 정리
표본의 크기인 n이 충분히 커진다면 모집단의 분포와 상관없이 표본 분포는 정규분포를 따른다.
여기서 충분한 크기인 n은 보통 30 이상이다.
'학교 > R프로그래밍' 카테고리의 다른 글
| R프로그래밍 기말고사 정리 04 - 연속확률분포에서의 중심극한정리 (0) | 2022.06.05 |
|---|---|
| R프로그래밍 기말고사 정리 -03 이산확률분포에서의 중심극한정리 (0) | 2022.06.05 |
| R프로그래밍 기말고사 정리 -정규성 검정 (0) | 2022.04.27 |
| R프로그래밍 중간고사 정리-14(난수 발생-연속확률분포) (0) | 2022.04.18 |
| R프로그래밍 중간고사 정리 -13 (난수 발생-이산형 분포) (0) | 2022.04.17 |
통계 이론은 이미 알고 있는 약간의 정보를 이용하여 미지의 상황을 파악하는데 도움을 주는 과학적인 방법이다. 미지의 상황이란 항상 확정적 사건이라기보다는 어떤 사건이 더 발생할 가능성이 많은가로 평가되어야 함은 당연하다.
그래서 확률의 개념은 매우 빈번하게 사용되고 있다.
그러나 정확한 확률을 계산한다는 것은 매우 지루하고 힘든 과정을 요한다.
그래서 어떤 사건이 일어날 수 있는 가능성을 표로 요약한 것을 확률분포라고 한다.
이러한 확률분포를 만들기 위해서는 각 사건이 일어날 가능성을 찾아야 하는데, 때론 이 과정이 매우 어렵다.
다행히 어떤 사건이 규칙성이 있어 수학적 함수로 표현 가능하다면 확률의 계산은 매우 편리할 것이며, 더욱이 이 수학적 함수가 우리 실생활에서 흔히 일어날 수 있는 사건과 유사하다면 매우 유용할 것이다. 이러한 유용한 함수를 확률분포 함수라 하며 정규분포, 이항 분포, 카이제곱 분포, t-분포, F-분포 등이 이미 유용하게 사용하고 있는 분포는 다양하다.
📕표본 분포
표본을 이용하기 때문에 발생하는 것으로 표본 통계량의 분포를 지칭한다. 표본을 뽑게 되면 뽑힌 자료를 이용하여 통계량을 계산할 수 있으나, 이 통계량의 값은 표본이 어떻게 뽑히느냐에 따라 달라질 것이다. 그래서 통계량은 확률변수가 되며 통계 이론에 의해 일정한 분포 함수를 갖게 된다.
📕모집단 분포의 추론
모집단에서 임의로 뽑은 표본(random sample)들의 분포가 모집단의 분포와 항상 비슷하게 나온다는 보장이 없다. 특히 표본이 개수가 적은 경우 표본의 분포로 모집단의 형태를 추론하기는 어렵다.
📕모수의 추론
모집단에서 실제로 관심을 갖는 것은 분포의 형태보다는 모수의 값이다. 모수를 추론하기 위하여 표본들을 적당한 형태로 변환한 표본들의 함수인 통계량(예를 들어 표본 평균, 표본 분산 등)을 구하게 된다. 그런데 이러한 통계량 값은 우리가 얻은 표본에 따라 매번 다른 값이 나올 것이다. 즉 통계량은 확률변수이며, 어떤 확률 분포를 따르게 된다.
📕통계량의 확률분포
표본을 이용하여 구한 통계량이 모수에 얼마나 근접한 값일까? 하는 의문은 당연히 발생한다. 왜냐하면 모수와 멀어져 있는 통계량은 가치가 없으며 그래서 대부분의 사람들은 통계량을 모수와 가까운 값으로 찾기를 원한다. 그래서 구한 통계량이 모수와 얼마나 다를까 혹은 같을까를 판단할 수 있는 방법이 필요하다.

📕중심 극한 정리
표본의 크기인 n이 충분히 커진다면 모집단의 분포와 상관없이 표본 분포는 정규분포를 따른다.
여기서 충분한 크기인 n은 보통 30 이상이다.
'학교 > R프로그래밍' 카테고리의 다른 글
| R프로그래밍 기말고사 정리 04 - 연속확률분포에서의 중심극한정리 (0) | 2022.06.05 |
|---|---|
| R프로그래밍 기말고사 정리 -03 이산확률분포에서의 중심극한정리 (0) | 2022.06.05 |
| R프로그래밍 기말고사 정리 -정규성 검정 (0) | 2022.04.27 |
| R프로그래밍 중간고사 정리-14(난수 발생-연속확률분포) (0) | 2022.04.18 |
| R프로그래밍 중간고사 정리 -13 (난수 발생-이산형 분포) (0) | 2022.04.17 |
