1.베르누이 시행 B(1,p)
- n이 1일때의 이항분포를 베르누이 시행이라고 한다.
○P(x)를 이용 plot을 사용
n=1; p=0.5; x=c(0:n)
y=dbinom(x,1,p)
plot(x,y,type="h",col="black",lwd=5,main="베르누이 시행B(1,p)")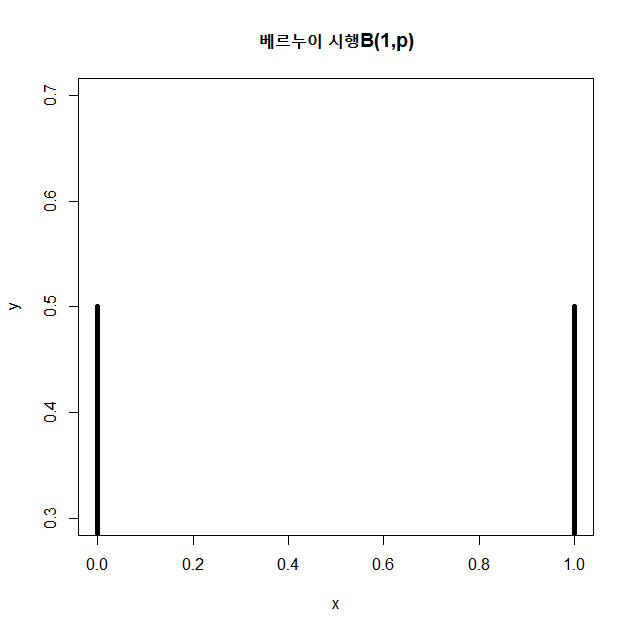
○난수를 이용 r~:난수 발생 type="h"
y=rbinom(10,1,0.3);y
[1] 0 0 1 0 1 0 0 0 0 1 ##B(1,0.3)에서 무작위 난수 10개가 발생된다.n=1;p=0.5;x=c(0:n)
##rbinom(size,n,p) B(n,p)에서 size개만큼 난수를 발생
rbinom(100,n,p) ## x,y순서쌍이 아닌 x값만 존재
##따라서 y값에 rbinom()값을 저장시킴.
y=rbinom(100,n,p)
mean(y);var(y)
plot(table(y),type="h",xlim=c(0,n),lwd=4)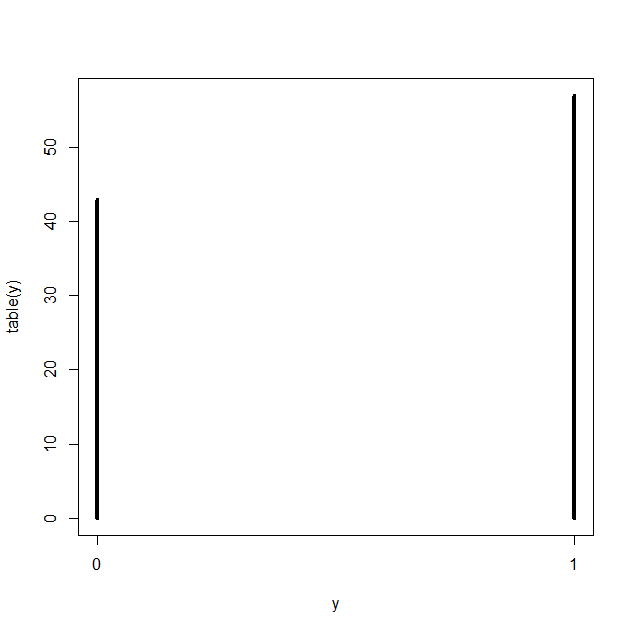
★그래프의 모양은 난수를 뽑아와서 그리는 것이기 때문에 그릴때마다 다른 모양을 나타낸다.
B(1,p) 그래프와 같아질려면 rbinom에서 어떻게 변화를 줘야할까?
정답은 난수의 개수를 무한하게 늘리면 된다. 집단의 개수가 커진다면 그래프는 모집단을 따라갈것이다.
n=1;p=0.5;x=c(0:n)
par(mfrow=c(2,2))
y=dbinom(x,n,p)
y1=rbinom(10,n,p)
y2=rbinom(50,n,p)
y3=rbinom(1000,n,p)
plot(x,y,type="h",xlim=c(0,n),lwd=4,col="green",main="크기가 1인 집단")
plot(table(y1),type="h",xlim=c(0,n),lwd=4,col="red",main="크기가 10인 집단")
plot(table(y2),type="h",xlim=c(0,n),lwd=4,col="blue",main="크기가 50인 집단")
plot(table(y3),type="h",xlim=c(0,n),lwd=4,col="yellow",main="크기가 1000인 집단")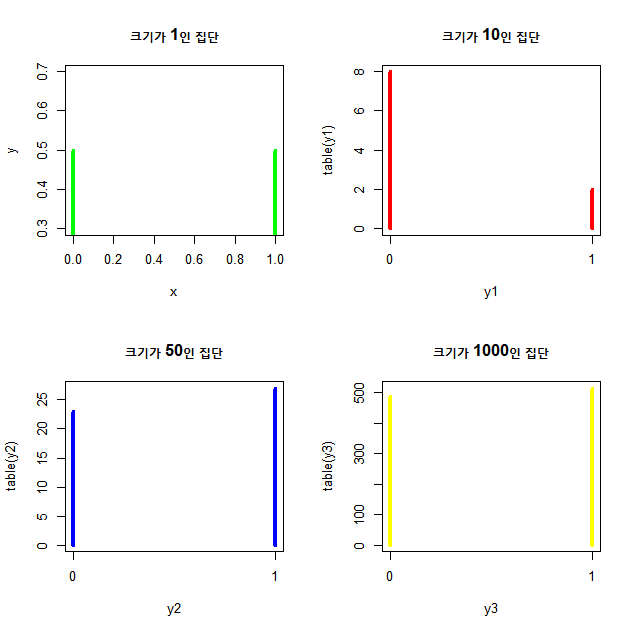
n이 커질수록 그래프의 모양이 크기가1인 원래의 그래프와 비슷해진다는 것을 볼 수 있다.
2.이항분포 B(n,p)
○p(x)를 이용
n=10;p=0.3;x=c(0:n)
y=dbiom(x,n,p)
plot(x,y,type="h",col="red",lwd=4,main="P(x)를 이용한 그래프")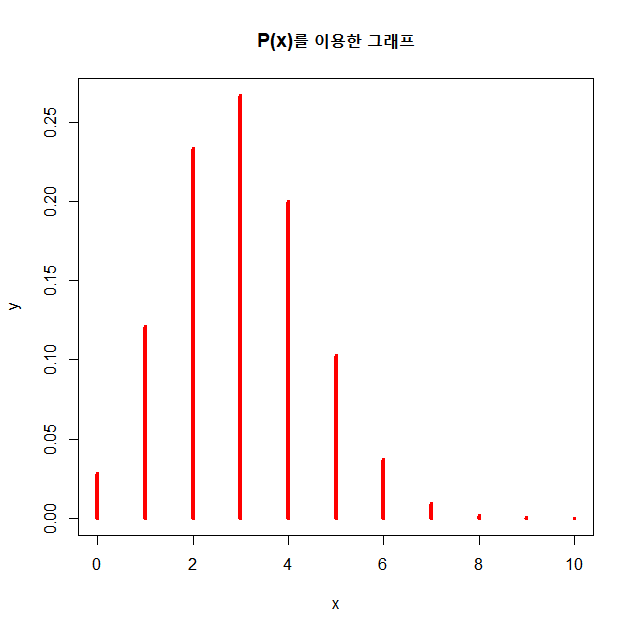
○난수를 이용 r~
rx=rbinom(10,n,p)
plot(table(rx),type="h",col="green",lwd=5,main="난수를 이용해서 만든 그래프")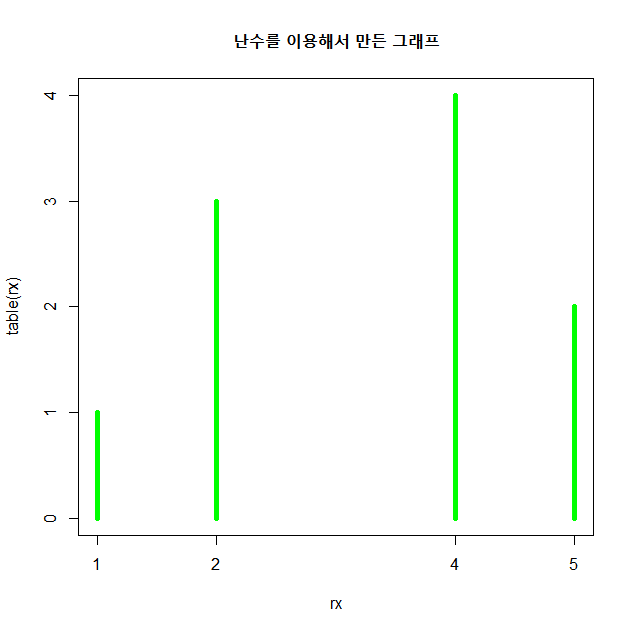
그래프를 보면 원래의 그래프와 모양이 많이 틀리다. 난수의 개수가 적기 때문이다.
그러면 위에서도 확인한것처럼 난수의 개수가 많아지면 원래의 그래프와 모양이 같아지는지 확인해보자.
rx=rbinom(10000,n,p)
plot(table(rx),type="h",col="green",lwd=5,main="크기가 10000인 난수 그래프")
##rbinom을 이용한 그래프는 type="h"로 그린다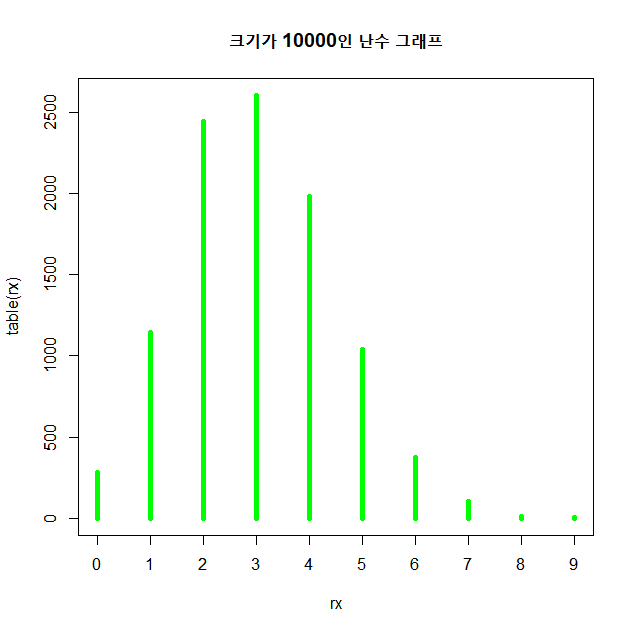
원래의 그래프 모양과 난수를 10000개 뽑아서 만든 그래프가 비슷하다고 볼 수 있다.
○난수집단 평균,분산 비교하기
ax=rbinom(10,n,p)
mean(ax);var(ax)
[1] 2.
[1] 1.566667
rx=rbinom(10000,n,p)
mean(rx);var(rx)
[1] 2.9742
[1] 2.095344
bx=rbinom(1000000,n,p)
mean(bx);var(bx)
[1] 3.000942
[1] 2.104517이항분포에서 평균은 np, 분산은 np(1-p)이다. 위 결과를 보면 n이 커질수록 평균은 3, 분산은 2.1에 가까워지는 것을 볼 수 있다.
3.Posion분포(포아송 분포)
●p(x)를 계산해서 그린 그래프
lambda=3;x=c(0:8)
y=lambda^x * exp(-1*lambda)/factorial(x) ## 포아송분포 공식
plot(x,y,type="h",col="blue",lwd=5,main="p(x)를 계산한 그래프")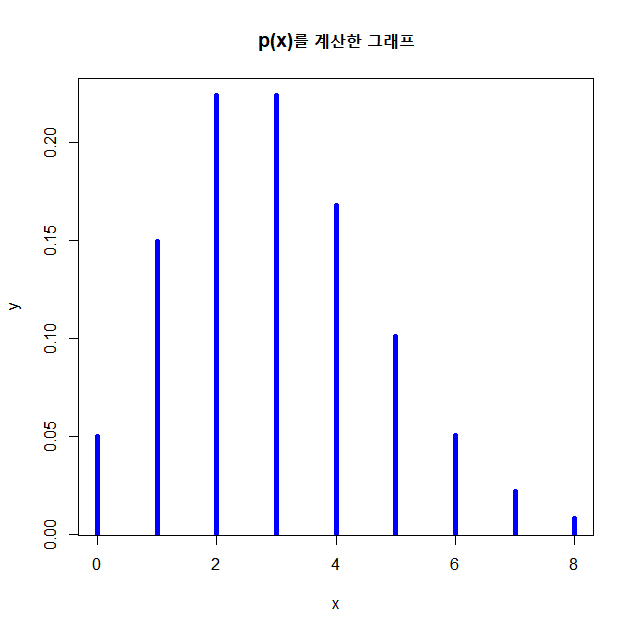
●난수를 이용 r~
lambda=3;x=c(0:8)
y=dpois(x,lambda)
ax=rpois(10,lambda)
bx=rpois(50,lambda)
cx=rpois(1000,lambda)
par(mfrow=c(2,2))
plot(x,y,type="h",col=1,lwd=5,main="원래 그래프")
plot(table(ax),type="h",col=2,lwd=5,xlim=c(0,8),main="크기가 10인 그래프")
plot(table(bx),type="h",col=3,lwd=5,xlim=c(0,8),main="크기가 50인 그래프")
plot(table(cx),type="h",col=4,lwd=5,xlim=c(0,8),main="크기가 1000인 그래프")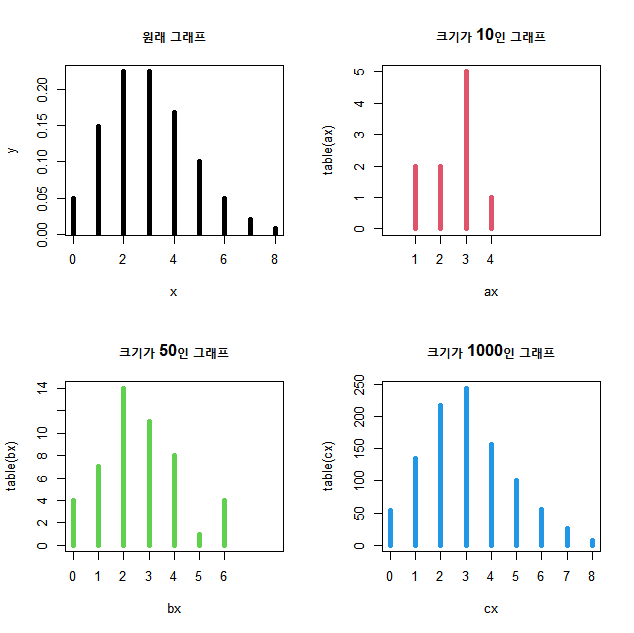
n값이 커질 수록 원래 그래프의 모양과 가까워지는 것을 볼 수 있다.
★난수 집단 평균,분산 비교하기
##lambda=3
mean(ax);var(ax)
[1] 2.5
[1] 0.9444444
mean(bx);var(bx)
[1] 2.78
[1] 3.522041
mean(cx);var(cx)
[1] 3.043
[1] 3.080231포아송 분포에서 평균과 분산은 lambda값이다. n이 커질수록 lambda값 3과 가까워지는것을 알 수있다!!.
'학교 > R프로그래밍' 카테고리의 다른 글
| R프로그래밍 기말고사 정리 -정규성 검정 (0) | 2022.04.27 |
|---|---|
| R프로그래밍 중간고사 정리-14(난수 발생-연속확률분포) (0) | 2022.04.18 |
| R프로그래밍 중간고사 정리-12 (확률 계산 및 그래프 그리기- t분포,카이제곱 분포) (0) | 2022.04.17 |
| R프로그래밍 중간고사 정리-11(확률 계산 및 그래프-정규분포) (0) | 2022.04.17 |
| R프로그래밍 중간고사 정리-10 (확률 계산 및 그래프-이항분포) (1) | 2022.04.17 |
