📕일양 분포 ( U(0,1))
par(mfrow=c(2,2))
n=c(10,100,1000,100000)
mu=0.5; var=1/12
for(j in 1: length(n))
{
m=1000
xbar=rep(0,m)
for( i in 1 : m){
x=runif(n[j])
xbar[i]=mean(x)}
xbar_mu = mean(xbar)
xbar_var= var(xbar);xbar_var
cat("표본의 개수 = ",n[j],"\n","모평균 = ",mu,"표본분포의 평균 = ",xbar_mu,"\n","모분산 = ",var,",var/n = ",var/n[j],"표본평균의 분산 = ",xbar_var,"\n")
hist(xbar,breaks="fd",prob=T)
curve(dnorm(x,mu,sqrt(var/n[j])),add=T)
}
📗표본의 개수가 늘어날수록 표본 분포의 평균과 분산이 모평균, 모 분산/n과 가까워짐을 알 수 있다.

📗m(xbar)가 충분히 큰 상태에서 n(표본의 개수)가 점점 증가할수록 표본 분포의 그래프 모양이 정규분포 형태를 따라간다.
✔ 정리
- 일양 분포는 중심 극한 정리가 성립한다.
- 표본의 개수가 증가할수록 표본 분포의 평균과 분산이 모평균,모분산/n과 가까워짐을 알 수있다.
- m(xbar)의 개수가 충분한 상태에서, 표본의 개수가 증가할수록 표본분포의 그래프 모양이 정규분포의 그래프 모양과 일치함을 알 수있다.
📕정규분포
par(mfrow=c(2,2))
n=c(10,100,1000,100000)
mu=10;var=25
for(j in 1: length(n))
{
m=1000
xbar=rep(0,m)
for( i in 1 : m){
x=rnorm(n[j],mu,sqrt(var))
xbar[i]=mean(x)}
xbar_mu = mean(xbar)
xbar_var= var(xbar);xbar_var
cat("표본의 개수 = ",n[j],"\n","모평균 = ",mu,"표본분포의 평균 = ",xbar_mu,"\n","모분산 = ",var,",var/n = ",var/n[j],"표본평균의 분산 = ",xbar_var,"\n")
hist(xbar,breaks="fd",prob=T)
curve(dnorm(x,mu,sqrt(var/n[j])),add=T)
}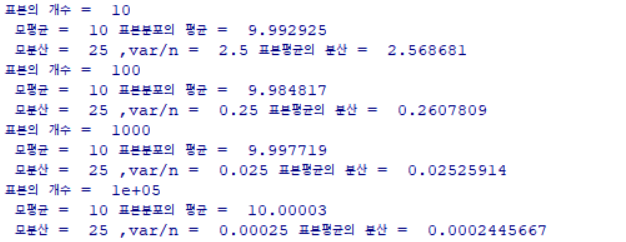
📗표본의 개수가 증가할수록 표본분포의 평균과 분산이 모평균, 모 분산/n과 가까워지는 것을 알 수 있다.
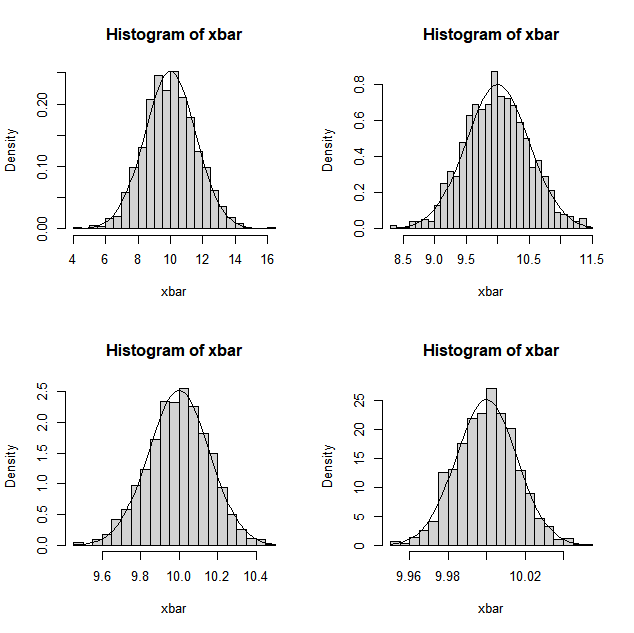
📗m(xbar)가 충분한 상태에서 표본의 개수(n)가 증가할수록 표본 분포의 그래프 모양이 정규분포와 가까워진다는 것을 알 수 있다.
✔정리
- 정규분포는 중심 극한 정리가 성립한다.
- 표본의 개수가 늘어날수록 표본 분포의 평균과 분산이 모평균,모분산/n과 가까워짐.
- m(xbar)가 충분한 상태에서 표본의 개수가 증가할수록 표본분포의 그래프 모양이 정규분포와 가까워짐.
📕지수 분포
par(mfrow=c(2,2))
n=c(10,100,1000,100000)
lambda=1; mu=1/lambda; var=1/lambda^2
for(j in 1: length(n))
{
m=1000
xbar=rep(0,m)
for( i in 1 : m){
x=rexp(n[j],lambda)
xbar[i]=mean(x)}
xbar_mu = mean(xbar)
xbar_var= var(xbar);xbar_var
cat("표본의 개수 = ",n[j],"\n","모평균 = ",mu,"표본분포의 평균 = ",xbar_mu,"\n","모분산 = ",var,",var/n = ",var/n[j],"표본평균의 분산 = ",xbar_var,"\n")
hist(xbar,breaks="fd",prob=T)
curve(dnorm(x,mu,sqrt(var/n[j])),add=T)
}
📗표본의 개수가 증가할수록 표본 분포의 평균과 분산이 모평균, 모 분산/n의 값과 가까워짐을 알 수 있다.
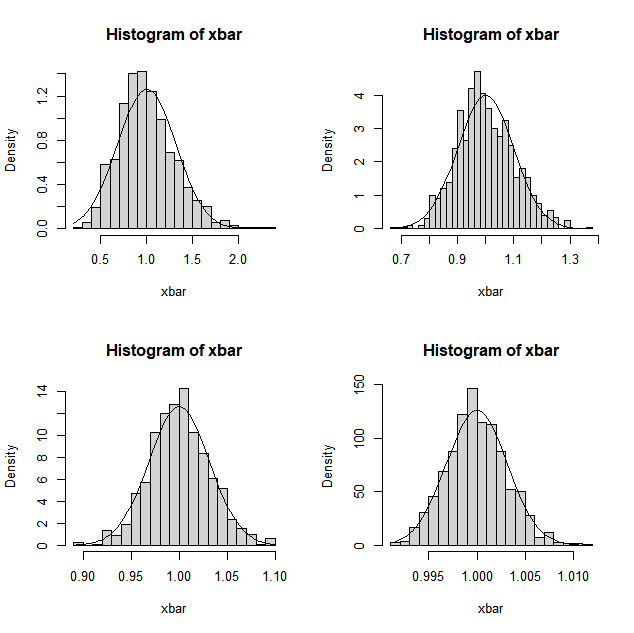
📗 m(Xbar)가 충분한 상태에서 n이 증가할수록 표본 분포의 그래프 모양이 정규분포의 형태와 가까워짐.
✔정리
- 지수 분포는 중심 극한 정리가 성립한다.
- 표본의 개수가 증가할수록 표본 평균과 표본 분산이 모평균, 모 분산/n과 가까워짐.
- 표본의 개수가 증가할수록 표본 분포의 그래프 모양이 정규분포의 형태를 따름.
'학교 > R프로그래밍' 카테고리의 다른 글
| R프로그래밍 기말고사정리06- 일표본 유의성 검정 (0) | 2022.06.05 |
|---|---|
| R프로그래밍 기말고사 정리 05- 데이터의 종류와 분석 (0) | 2022.06.05 |
| R프로그래밍 기말고사 정리 -03 이산확률분포에서의 중심극한정리 (0) | 2022.06.05 |
| R프로그래밍 기말고사 정리 -02 중심극한정리 (0) | 2022.06.04 |
| R프로그래밍 기말고사 정리 -정규성 검정 (0) | 2022.04.27 |
📕일양 분포 ( U(0,1))
par(mfrow=c(2,2)) n=c(10,100,1000,100000) mu=0.5; var=1/12 for(j in 1: length(n)) { m=1000 xbar=rep(0,m) for( i in 1 : m){ x=runif(n[j]) xbar[i]=mean(x)} xbar_mu = mean(xbar) xbar_var= var(xbar);xbar_var cat("표본의 개수 = ",n[j],"\n","모평균 = ",mu,"표본분포의 평균 = ",xbar_mu,"\n","모분산 = ",var,",var/n = ",var/n[j],"표본평균의 분산 = ",xbar_var,"\n") hist(xbar,breaks="fd",prob=T) curve(dnorm(x,mu,sqrt(var/n[j])),add=T) }

📗표본의 개수가 늘어날수록 표본 분포의 평균과 분산이 모평균, 모 분산/n과 가까워짐을 알 수 있다.

📗m(xbar)가 충분히 큰 상태에서 n(표본의 개수)가 점점 증가할수록 표본 분포의 그래프 모양이 정규분포 형태를 따라간다.
✔ 정리
- 일양 분포는 중심 극한 정리가 성립한다.
- 표본의 개수가 증가할수록 표본 분포의 평균과 분산이 모평균,모분산/n과 가까워짐을 알 수있다.
- m(xbar)의 개수가 충분한 상태에서, 표본의 개수가 증가할수록 표본분포의 그래프 모양이 정규분포의 그래프 모양과 일치함을 알 수있다.
📕정규분포
par(mfrow=c(2,2)) n=c(10,100,1000,100000) mu=10;var=25 for(j in 1: length(n)) { m=1000 xbar=rep(0,m) for( i in 1 : m){ x=rnorm(n[j],mu,sqrt(var)) xbar[i]=mean(x)} xbar_mu = mean(xbar) xbar_var= var(xbar);xbar_var cat("표본의 개수 = ",n[j],"\n","모평균 = ",mu,"표본분포의 평균 = ",xbar_mu,"\n","모분산 = ",var,",var/n = ",var/n[j],"표본평균의 분산 = ",xbar_var,"\n") hist(xbar,breaks="fd",prob=T) curve(dnorm(x,mu,sqrt(var/n[j])),add=T) }

📗표본의 개수가 증가할수록 표본분포의 평균과 분산이 모평균, 모 분산/n과 가까워지는 것을 알 수 있다.

📗m(xbar)가 충분한 상태에서 표본의 개수(n)가 증가할수록 표본 분포의 그래프 모양이 정규분포와 가까워진다는 것을 알 수 있다.
✔정리
- 정규분포는 중심 극한 정리가 성립한다.
- 표본의 개수가 늘어날수록 표본 분포의 평균과 분산이 모평균,모분산/n과 가까워짐.
- m(xbar)가 충분한 상태에서 표본의 개수가 증가할수록 표본분포의 그래프 모양이 정규분포와 가까워짐.
📕지수 분포
par(mfrow=c(2,2)) n=c(10,100,1000,100000) lambda=1; mu=1/lambda; var=1/lambda^2 for(j in 1: length(n)) { m=1000 xbar=rep(0,m) for( i in 1 : m){ x=rexp(n[j],lambda) xbar[i]=mean(x)} xbar_mu = mean(xbar) xbar_var= var(xbar);xbar_var cat("표본의 개수 = ",n[j],"\n","모평균 = ",mu,"표본분포의 평균 = ",xbar_mu,"\n","모분산 = ",var,",var/n = ",var/n[j],"표본평균의 분산 = ",xbar_var,"\n") hist(xbar,breaks="fd",prob=T) curve(dnorm(x,mu,sqrt(var/n[j])),add=T) }

📗표본의 개수가 증가할수록 표본 분포의 평균과 분산이 모평균, 모 분산/n의 값과 가까워짐을 알 수 있다.

📗 m(Xbar)가 충분한 상태에서 n이 증가할수록 표본 분포의 그래프 모양이 정규분포의 형태와 가까워짐.
✔정리
- 지수 분포는 중심 극한 정리가 성립한다.
- 표본의 개수가 증가할수록 표본 평균과 표본 분산이 모평균, 모 분산/n과 가까워짐.
- 표본의 개수가 증가할수록 표본 분포의 그래프 모양이 정규분포의 형태를 따름.
'학교 > R프로그래밍' 카테고리의 다른 글
| R프로그래밍 기말고사정리06- 일표본 유의성 검정 (0) | 2022.06.05 |
|---|---|
| R프로그래밍 기말고사 정리 05- 데이터의 종류와 분석 (0) | 2022.06.05 |
| R프로그래밍 기말고사 정리 -03 이산확률분포에서의 중심극한정리 (0) | 2022.06.05 |
| R프로그래밍 기말고사 정리 -02 중심극한정리 (0) | 2022.06.04 |
| R프로그래밍 기말고사 정리 -정규성 검정 (0) | 2022.04.27 |
