📕문제
아래 그림과 같이 삼각형 모양으로 숫자를 쌓기로 했다.
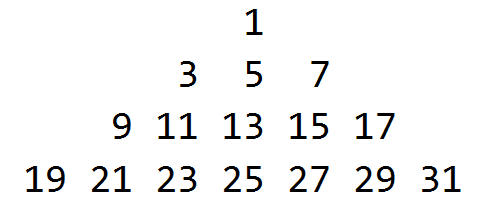
위와 같이 경표는 끝도 없이 피라미드를 쌓을 때, N층의 제일 왼쪽, 오른쪽에 쓰게 될 숫자가 무엇일지 예측해보자.
📕입력
첫 번째 줄에 테스트 케이스의 수 T가 주어진다.
각 테스트 케이스의 첫 번째 줄에는 층의 번호 N(1≤N≤109)이 주어진다.
📕출력
각 테스트 케이스마다 ‘#x’(x는 테스트 케이스 번호를 의미하며 1부터 시작한다)를 출력하고,
각 테스트 케이스마다 N층의 제일 왼쪽, 오른쪽에 쓰게 될 숫자를 공백으로 구별하여 출력한다
📗입력 예시
| 3 1 2 3 |
// 테스트 케이스 개수 // 첫 번째 테스트 케이스, N = 1, K = 1 // 두 번째 테스트 케이스, N = 3, K = 7 // 세 번째 테스트 케이스, N = 9, K = 17 |
📗출력 예시
| #1 1 1 #2 3 7 #3 9 17 |
// 첫 번째 테스트 케이스 결과 // 두 번째 테스트 케이스 결과 // 세 번째 테스트 케이스 결과 |
정리
- 삼각형은 희소행렬의 모양이다.
- n층의 원소의 개수는 1+2(n-1) 개다.
- n층까지의 총 원소 개수는 2^n이다.
- n층의 왼쪽의 원소들과 오른쪽의 원소를 구해야 한다.
- n층의 왼쪽의 원소는 n-1층까지의 원소의 개수만큼 1과 떨어져 있다.
- n-1층까지의 총원소의 개수는 2^(n-1)이다.
- 따라서 n층 왼쪽의 원소는 2*(n-1)^2+1이다.
- n층의 오른쪽 원소는 1부터 n층의 원소의 개수-1만큼 떨어져 있다.
- n층의 원소의 개수는 2^n이다.
- 따라서 n층 오른쪽의 원소는 2*n^2-1이다.
- n층의 왼쪽의 원소는 n-1층까지의 원소의 개수만큼 1과 떨어져 있다.
💡코드
/*
홀수 피라미드 문제
1층에는 1개 , 2층에는 3개 3층에는 5개 4층에는 7개 등등 등차수열로 증가함.
n층은 1+2*(n-1)개의 사다리가 나올것이다.
왼쪽은 층의 원소수 * 2만큼 차이난다.
4층일때 원소의 갯수는 1+3+5+7 = 16
3층일때 원소의 갯수는 9 층의제곱수만큼 원소가 있다.
만약의 5층이면 1+2*n()
왼쪽 오른쪽 숫자 출력.
*/
#include <iostream>
#include <vector>
#include <algorithm>
#include <math.h>
using namespace std;
vector<unsigned long long int> l;
vector<unsigned long long int> r;
void solve(int high);
int main()
{
int T;
cin >> T;
unsigned long long int high;
vector<int> H;
unsigned long long int m = 0;
H.resize(T);
long long int left, right;
for (int i = 1; i <= T; i++)
{
cin >> high; // high층일때를 구해야함.
if (high == 1)
{
left = 1, right = 1;
}
else
{
left = (high-1)*(high-1)*2 + 1;
right = 2*(high)*(high)-1;
}
cout << "#" << i << " " << left << " " << right << endl;
}
}
문제출처
https://swexpertacademy.com/main/code/problem/problemDetail.do?contestProbId=AWvzGUKKPVwDFASy
'Skils > Algorithm' 카테고리의 다른 글
| [알고리즘 기말 이론] (0) | 2022.06.15 |
|---|---|
| [알고리즘] Intractability & NP-Theory (0) | 2022.06.13 |
| [알고리즘-C++] 계산복잡도 (0) | 2022.05.31 |
| [알고리즘-C++] - 외판원 순회 문제(Branch & Bound) (1) | 2022.05.31 |
| [알고리즘-C++] 외판원 순회 문제(Dynamic Programming) (0) | 2022.05.29 |
