💡Intractability
사전적인 의미로는 취급하거나 작업하기 어렵다는 뜻이다.
CS적인 관점에서는 문제가 Intractable하다는 뜻은 polynomial-time-algorithm(다차시간 알고리즘)으로 못푼다는 의미이다.
polynomial-time algorithm은 최악 시간복잡도의 상한이 입력크기의 다항식 함수가 되는 알고리즘이다.
다루기 힘든 정도는 문제를 푸는 어떤 특정 알고리즘의 성질이 아니라 문제의 성질이라는 사실을 반드시 알아야한다.
다루기 힘든 정도에 대하여 3가지 종류로 문제를 분류할 수 있다.
1.다차시간 알고리즘을 찾은 문제
2.다루기 힘들다고 증명된 문제
3.다루기 힘들다고 증명되지도 않았지만, 다차시간 알고리즘도 찾지 못한 문제(NP-complete)
예를 들어 TSP문제에서
아무도 TSP문제를 다차시간 알고리즘으로 해결하지못했다.
하지만 다차시간 알고리즘으로 해결하는것이 불가능하다고도 아무도 증명하지 못했다.
--> 이런 문제를 (NP-complete)라고한다.
Input Size Revisited
지금까지의 알고리즘에서는 보통 n을 입력크기로 보았다. 왜냐하면 n은 입력 데이터의 크기를 나타내는 척도로서 적당했기 때문이다. 예를 들어 정렬 알고리즘의 경우 정렬할 키의 개수인 n은 입력데이터의 크기를 나타내는 좋은 척도이다.
따라서 n을 입력크기라고하였다.
그러나 n이 무조건 알고리즘의 입력크기가 되는 건 아니다.
그에 대한 예시가 바로 n이 소수인지 검사하는 알고리즘이다.
bool prime(int n){
int i; bool flag;
flag=true;
i=2;
while(flag&& i<=(int)floor(sqrt(n)))
if(n%i==0)
flag=false;
else
i++;
return flag;
}이 코드에서 while루프의 실행횟수는 분명 ϴ(√n)이다.
그러나 이 알고리즘을 다차시간 알고리즘이라고 할 수있을까?
n이 알고리즘의 입력이긴 하지만 입력크기라고 할 수 없다. 즉 n 값은 입력사례일 뿐이다.
정렬알고리즘에서 n은 입력크기이자 key의 개수지만 소수를 구하는 알고리즘에서는 n은 입력크기라고 볼수없다.
소수판별알고리즘에서는 입력크기는 입력을 작성하는데 필요한 문자의 개수로 정의한다.
일반적으로 소수판별 알고리즘에서 입력은 n하나이다.
n이 커진다면 n의 정보량도 증가한다.(bit수)
bit는 log2 N이다.
즉 시간복잡도는 2^(lgn)이다.
-->다차시간 알고리즘이 아님.
소수검사 알고리즘 같은 알고리즘에서 n을 입력의 절대크기라고한다.
소수검사알고리즘에서 n은 숫자를 의미하고, 입력사이즈는 n의 비트수를 의미한다.
최악 시간복잡도 W(s)는 입력크기 s에 대하여 그 알고리즘이 실행할 다누이연산의 최대개수이다.
최악시간복잡도의 상한이 크기와 절대크기로 모두 다차시간이 되는 알고리즘을 의사다차시간(Pseudopolynomial-time)이라한다.
다차시간 알고리즘을 찾은 문제
n이 알고리즘의 입력 데이터 크기를 나타내는 알고리즘들은 모두 다차시간이다.
ex)sort, 정렬된 배열 검색, 해열ㄹ곱셈,연쇄행렬곱셈
다루기 힘들다고 증명된 문제(NP-Hard)
두가지 종류의 문제가 있다.
1.지수이상 크기의 출력을 요구하는 문제이다.
ex) 해밀톤 회로 문제.
2.요구가 현실적이고(지수시간 이상 크기의 출력 요구x), 문제를 다차시간에 풀 수없다고 증명할 수 있는 경우이다.)
ex)진위판별불가능(undecidable)
대표적인 예 : Halting problem(정지 문제)
---
지금까지 다루기 힘들다고 증명된 문제는 NP집합에 속하지 않는다고 증명되었다.
그러나 다루기 힘들 것처럼 보이는 문제는 대부분 NP집합에 속한다.
다루기 힘들다고 증명되지도 않았고, 다차 시간 알고리즘도 찾지 못한 문제
ex) 해답을 하나만 내주도록 문제를 기술하면
0-1 knapsack, TSP, subset_sum,m-coloring,해밀톤 회로문제 등이 있다.
사례를 임의의 제한된 부분집합에서 취할 떄 단위연산을 수행하는 횟수의 한계를 정하는 n에 대한 다항식(polynomial)이 존재한다. 그러나 모든 사례에 대하여 다항식이 존재하는 것은 아니다.
NP-theory
결정문제와 최적화 문제가 있다.
결정문제의 output은 간단하게 yes or no로 답할 수 있는 문제.
최적화 문제의 output은 최적의 방법이다.
최적화 문제는 모두 각각에 대응되는 결정문제가 존재한다.
TSP
최적(opt) : 이음선 상 총 거리가 최소가 되는 여행경로를 구하는 문제.
결정(dec) : 임의의 양수 d가 주어지고, 총 거리가 d보다 길지 않은 여행경로가 있는지 판별하는 문제.
0-1 knapsack
최적(opt) : 배낭에 넣을 아이템의 가치의 합이 최대가 되도록 아이템을 배낭에 어떻게 채울지를 알아내는 문제.
결정(dec): 총 무게가w가 넘지 않으면서 총 수익이 최소한 P가 되도록 배낭을 채울 수 있는지 판별하는 문제
M-Coloring
최적(opt): 인접한 두 마디가 같은 색이 되지 않도록 그래프를 색칠하는데 필요한 색의 최소 가지 수를 구하는 문제.
결정(dec): 최대한 m가지 색을 사용하여 인접한 두 마디가 같은 색이 되지 않도록 그래프를 색칠할 수 있는지 판별하는 문제.
위 문제들에 대해서 결정문제와 최적화 문제 모두 다차시간 알고리즘을 아직 찾지 못했다.
그러나 어느 한 문제라도 최적화 문제에 대한 다차시간 알고리즘을 찾을 수 있다면 그에 대응하는 결정 문제에 대한 다차시간 알고리즘도 존재할 것이다.
왜냐하면 최적화 문제에 대한 해답을 구하면 ,그에 상응하는 결정 문제에 대한 해답은 쉽게 얻을 수 있기 때문이다.
최적화 문제를 푸는 다차시간 알고리즘을 가지고 그에 대응하는 결정 문제를 푸는 다차시간 알고리즘을 자동으로 만들어낼 수 있으므로 초기에는 결정 문제만 가지고 이론을 전개할 수있다.
따라서 결정문제를 살펴보고 다음에 최적화 문제를 살펴보는것이 맞다.
P와 NP집합
P는 다차시간 알고리즘으로 풀 수 있는 모든 결정문제의 집합이다.
다차시간으로 풀지 못한 문제가 있을 때 그 문제가 다차시간 알고리즘으로 풀 수 없다고 증명한 사람도 아직 없다. 따라서 그 문제는 P에 속할 가능성이 있다.
따라서 결정문제가 P에 속하지 않음을 확실히 증명할려면 그 문제를 푸는 다차시간 알고리즘이 존재하지 않다는 것을 증명해야한다. 외판원 결정문제에 대해서는 아무도 이를 증명하지 못했다.+(0-1 knapscak, M-Coloring)
NP집합에 속하는 문제들이 지니고 있는 다차시간 검증가능성(polynomial-time - verifiability)
이 문제들을 다차시간에 풀어야 한다는 의미는 아니다.
검증만 하는데 다차시간이 걸렷다는 것 뿐.
비결정 알고리즘
1.(비결정)추측단계
2.(결정)검증단계
다차시간 비결정 알고리즘은 검증단계가 다차시간 알고리즘인 비결정 알고리즘이다.
NP는 다차시간 비결정적 알고리즘으로 풀 수 있는 모든 진위판별 문제의 집합이다.
NP의 약자는 Nondeterministic(비결정) + Polynomial(다차)
P에 속하는 문제는 모두 NP에 속한다.
NP에 속하지 않는다고 증명된 결정문제들은 다루기 힘들다고 증명된 문제들이다.ex) Halting-problem
진위판별 문제의 집합
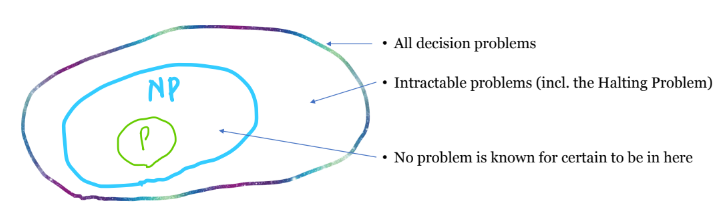
NP는 P를 진부분집합으로 포함하고 있는 걸로 그렸다. 그러나 아닐 수도 있다.
즉 NP에 속하면서 P에 속하지 않는 문제가 있다고 아직 증명하지 못했기 때문이다.
if ( P = NP) 결정문제를 푸는 다차시간 알고리즘이 존재한다는얘기
if( P !=NP) NP에 속하면서 P에는 속하지 않는 문제를 찾아야한다.
CNF-Satisfiability Problem
CNF 논리식의 logical variable은 true와 false값중 하나를 가질 수 있는 변수이다.
x_는 x의 부정이다.
literal(리터럴)은 논리변수이거나 본리변수의 부정이다.
clause(절)은 논리연산자 or를 사이사이에 끼운 리터럴의 나열이다.
CNF는 논리식으로 논리연산자 and를 사이사이에 끼운 절의 나열이다.
CNF논리식의 예
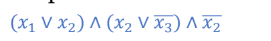
위 문제의 대해서 x1= true, x2= false, x3=false를 대입하면 논리식이 true이기때문에 CNF-Satisfiability 문제의 답은 "예"이다.
또다른 예시를 들어보겠다.

위 문제에 대해서는 true가 되는 x1,x2가 없기 때문에 CN-Satisfiability 문제의 답은 "아니오"이다.
CNF-Satiafiability 결정문제는 주어진 CNF 논리식을 true로 만드는 참값 대입(변수에 true 또는 false를 대입)이 존재하는지 판별하는 문제이다.
CNF-Satiafiability은 NP에 속한다.
그러나 CNF-Satiafiability 문제를 푸는 다차시간 알고리즘을 아직 아무도 찾지 못했고, 이 문제를 다차시간에 풀 수 없다고 아직 아무도 증명하지 못했다. 따라서 이 문제는 P에 속할지도 모른다.
이 문제가 중요한 이유는 Cook의 이론에서 CNF-Satiafiability가 P에 속한다고 가정하면 P=NP가 사실임을 증명하는 논문을 발표했기 때문이다.
Transfromation Algorithm
결정문제 A의 모든 사례를 문제 B의 사례로 실제로 매핑하는 함수이다.
다차시간 다일 축소변환가능 정의
결정문제 A를 결정문제 B로 변환하는 다차시간 변환 알고리즘이 존재하면 문제A는 문제B로 다차시간 다일 축소변환가능하다라고 한다.
A∝B라고 표현한다.
NP-complete
두 조건을 만족하면 NP-Complete라고 한다.
1.Np에 속한다.
2.NP에 속한 모든 다른 문제 A , A->B로 변환이 가능하다면 NP-Complete라고한다.
CNF-Satiafiability는 NP-Complete이다.
CNF-Satiafiability∝해밀턴 회로 결정 문제도 ∝(비방향)외판원 결정 문제 ∝ 외판원 결정 문제
-->모두 NP-Complete
만약 C가 NP에 속하고 다른 NP-Complete문제 B에 대해서 B∝C(변환가능하다면 ) C는 NP-Complete이다.
NP-Complete에 속하면 서로 변환이 가능하다는 뜻이다.
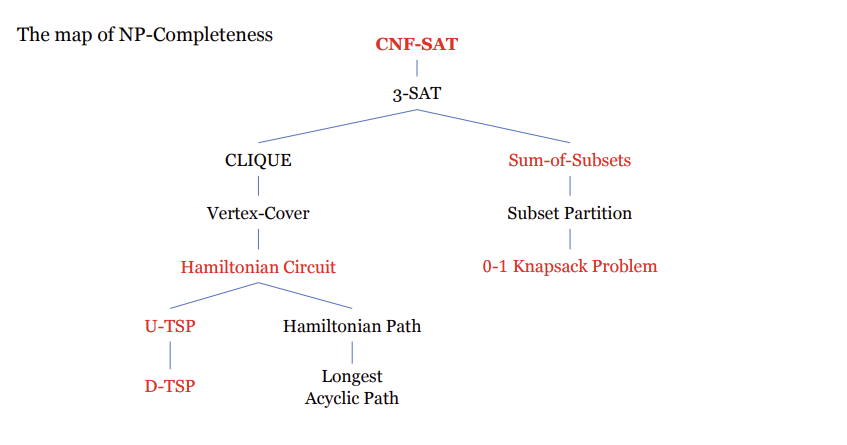
NP문제는 모두 NP-Hard문제로 축소변환 가능하다.
A(임의의 NP-Complete) is Turing reducible to B라면 B는 NP-Hard라고 한다.
NP-Complete문제는 모두 NP-Hard문제이다.
최적화문제(NP-Complete인)는 NP-Hard이다. 여기서 최적화 문제는 결정문제로 바꿀수 있어야한다.
외판원 최적화 문제는 NP-Hard이다.
Handling NP-Hard Problems
근사알고리즘을 사용
N이 너무 클경우는 최적값을 찾는걸 포기함.
-이 알고리즘은 최적값을 구한다고 보장할 수는 없다.
하지만 다른 방법보다는 최적값과 가깝게 이끌어낸다.
bound의 개념 사용
구한해가 얼마나 최적에 가까운지를 보장해주는 범위값
TSP 근사 알고리즘
최소비용 신장트리를 구한다.
트리를 두 번 횡단하여 모든 도시를 방문하는 경로를 구축한다.
지름길을 택하여 마디를 두 번 방문하지 않은 경로(즉, 여행경로를 구축한다)
정리포기~~!!
'Skils > Algorithm' 카테고리의 다른 글
| [알고리즘] DFS & BFS (0) | 2022.07.30 |
|---|---|
| [알고리즘 기말 이론] (0) | 2022.06.15 |
| [알고리즘 기말예제문제] 홀수피라미드(C++) (0) | 2022.06.12 |
| [알고리즘-C++] 계산복잡도 (0) | 2022.05.31 |
| [알고리즘-C++] - 외판원 순회 문제(Branch & Bound) (1) | 2022.05.31 |
