알고리즘에 도전해보는 방식 2가지
1. 문제를 푸는 더 효율적인 알고리즘을 설계하기
2. 더 효율적인 알고리즘 개발이 불가능함을 증명하기
계산 복잡도는 주어진 문제를 풀 수 있는 가능한 모든 알고리즘에 대한 연구이다.
문제를 푸는 모든 알고리즘의 효율성(복잡도)의 하한을 구하는 것이다.
과연 이 알고리즘이 최선일까? 더 효율적인 알고리즘은 없는가?를 연구하는 것
Finding the Largest Key :
Problem : Find the largest key in the arrays of size n, indexed from 1 to n
Outputs : variable large, whose value is the largest key in S.
void find_largest(int n, vector<int>S, int&large){
int i;
large=S[1];
for(i=2; i<=n;i++)
{
if(S[i]>large){
large=S[i];
}
}
}해당 알고리즘의 T(n)= n-1이다.
직관적으로 배열에서 가장 큰 키를 찾는 과정에서 위 알고리즘보다 더 효율적인 알고리즘은 찾을 수 없다.
만약 배열이 정렬된 상태라면 오름차순일때는 마지막 원소를, 내림차순일 때는 첫 원소를 반환해주면 되지만 문제의 조건은 정렬되어있지 않은 배열 이어야 한다.
그래서 Finding the largest key의 lower bound는 n-1이라고 우리는 정의할 수 있다.
Finding Both the Smallest and Largest Keys
problem : find the smallest and largest keys simultaneously
->위의 find largest keys의 알고리즘을 일부분 수정하면 만들 수 있다.
void find_both(int n, vector<int>S,int &small,int &large)
{
int i;
small=S[1];
large=S[1];
for ( i=2; i<=n;i++)
{
if(S[i]<small)
small=S[i];
else if(S[i]>large)
large=S[i];
}
}이 알고리즘은 최솟값과 최댓값을 독립적으로 찾는 알고리즘보다 효율적이다.
왜냐하면 S [i]의 large를 찾을 때 모든 i에서 비교하지 않기 때문이다.
하지만 최악의 경우에 S [1]이 가장 작은 값이라면
모든 i에서 비교를 해야 한다. (if문은 항상 false기 때문에 else if를 검사함.)
따라서 if, else if 검사 : 2번, 첫 원소를 제외한 모든 원소를 검사하기 때문에 2(n-1)이라 W(n)=2n-2가 된다.
이 알고리즘은 더 이상 효율성을 향상할 수 없어 보이지만 실제로는 그렇지 않다.
어떻게?
void find_poth_pair(int n, vector<int>S,int &small,int &large)
{
int i;
if(S[1]<S[2]){
small=S[1],large=S[2];
}
else {
small=S[2],large=S[1];
}
for(i=3;i<=n-1;i+=2)
{
if(S[i]<S[i+1]){
if(S[i]<small) small=S[i];
if(S[i+1]>large) large=S[i+1];
}
else{
if(S[i+1]<small) small=S[i+1];
if(S[i]>large) large=S[i];
}
}
}--> 2개씩 짝을 지어서 서로 비교한 뒤 작은 키는 small에 큰 키는 large에 넣는다. (토너먼트 형식과 동일함)
여기서 소요되는 T(n)= n/2이다. (여기서 원소의 개수 n은 짝수라고 가정한다.)
large에 원소의 개수는 n/2, small에 원소의 개수는 n/2일 것이다.
large 집합에서 가장 큰 원소를 찾기 위해서는 (n/2)-1, small 집합에서 가장 작은 원소를 찾기 위해서는 (n/2)-1이 소요될 것이다.
따라서 총 T(n)= 3n/2 -2가 될것이다. --만약 n이 홀수라면 T(n)=3n/2-3/2이다.
이렇게 분석을 했다면 최종적으로 우리는 또 질문을 해야 할 것이다.
이것보다 더 효율적인 알고리즘이 있을까?
정답은 더 효율적은 알고리즘은 더 이상 없다.
그걸 어떻게 판단하냐?
--> adversary argument라는 기법을 써서 문제의 lower bound를 결정한다.
Adversary Argument
- 당신이 만약 adversary가 된다면 yes or no 질문에만 대답할 수 있다.
- 당신은 제대로 된 대답을 해야 할 의무는 없다.
- 그러므로 당신은 가능한 많은 질문을 하도록 대답해야 할 것이다.
- 당신의 대답에 요구조건은 그 대답들이 일관성을 유지해야 할 것이다.
- 따라서 당신의 대답의 목적은 최대한 모든 가능성을 열어주는 대답을 해야 할 것이다.
Adversary의 목표를 알고리즘을 가능한 어렵게 만드는 것이라고 가정하자.
알고리즘이 결정을 해야 하는 지점에서 당신은 가능한 알고리즘이 느려지게 되는 결정을 선택하려고 노력해야 할 것이다.
제한사항은 당신은 언제나 일관된 대답을 해야 한다는 점이다.
만약 당신이 한 알고리즘을 F(n) times가 되도록 만들었다면
그 F(n)은 worst-case tiem complexity의 lower bound가 될 것이다.
Finding Both Problem에 Adversary Argument를 적용해보자.
lower bound를 얻기 위해서는 최솟값과 최댓값을 찾아야 한다.
여기서 key들은 중복되지 않았다고 가정한다.
단순 key들의 비교만으로 최댓값과 최솟값을 찾는 알고리즘을 푼다고 가정하자.
전략은 이렇다
key들의 상태는 4가지로 나타난다.

X : 아직 비교하지 않은 key
L : 비교를 했고, 아직 한 번도 이기지 못한 key
W : 비교를 했고, 아직 한번도 진적 없는 key
WL : 비교를 했고, 이긴 적도 있고 진적도 있는 key
각 상태별로 얻을 수 있는 정보는
X는 아직 비교를 하지 않았기 때문에 정보는 0이고, L과 W는 한 번의 비교를 했기 때문에 얻을 수 있는 정보량은 1이며,
WL은 비교를 해서 이기기도 했고, 지기도 했기 때문에 알 수 있는 정보량은 2이다.
모든 키들은 smallest key에게 한 번씩 이기고, largest key에게 한번씩 진다.
따라서 알고리즘은 2n-2의 비교를 하게 된다.
우리의 전략은 알고리즘을 가능한 어렵게 만드는 것이다.
그러므로 우리는 각 비교에서 최소한의 정보를 제공해야 할 것이다.
예를 들어 s1과 s2를 비교한다고 할 때 2개의 정보가 노출될 것이다.
어느 대답을 하던 중요한 건 아니지만 s2가 크다고 가정하자.
그럼 s2의 상태는 W고 s1의 상태는 L로 2개의 정보를 얻을 수 있다.
다음 s2과 s3을 비교한다고 가정하자.
s3이 클 경우 두 개의 정보가 노출된다. --> s3 : X->W, s2 : W -> WL
s2이 클 경우 하나의 정보가 노출된다. --> s3 : X->L, s2 : W (s2의 상태는 그대로 이므로 하나의 정보만 노출)
따라서 우리는 무조건 정보가 적게 노출되는 전략을 택하기에 s2이 s3보다 크다고 대답해야 할 것이다.
void find_both(int n, vector<int>S,int &small,int &large)
{
int i;
small=S[1];
large=S[1];
for ( i=2; i<=n;i++)
{
if(S[i]<small)
small=S[i];
else if(S[i]>large)
large=S[i];
}
}해당 알고리즘을 따른다.
그리고 S=[10,20,30,40,50]이다.
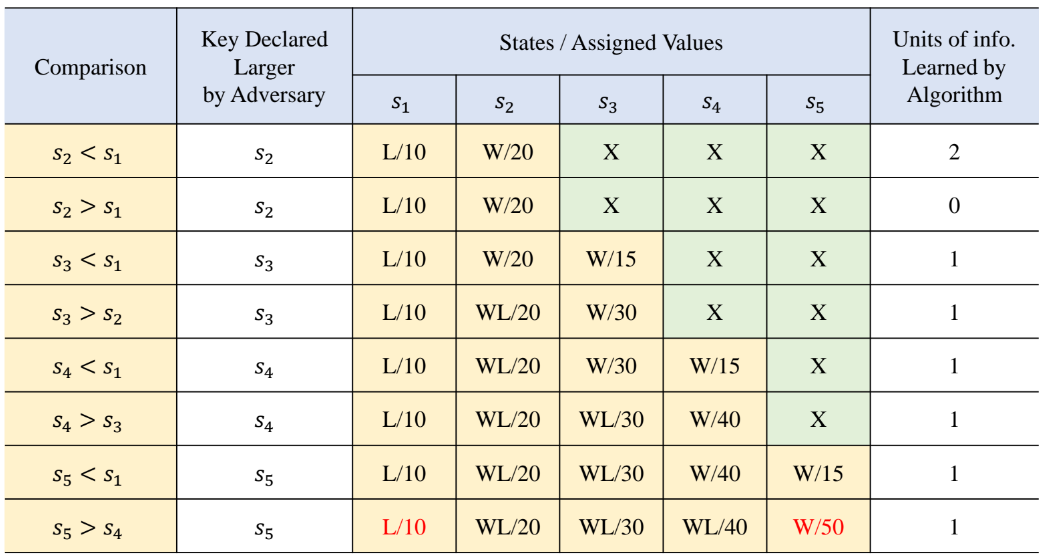
알고리즘 실행 결과 S1이 smallest key가 되고, S5가 largest key가 될 것이다.
n=5라서 비교는 총 8번이 이루어졌다.
원래 가장 효율적인 비교는 n이 5기 때문에 T(n)=3/2n - 3/2에 대입하면 6번의 비교가 최소의 비교지만
우리의 방해 전략으로 비교가 8번 이루어졌기 때문에 방해가 성공했다고 할 수 있다.
Finding the Second-largest key :
가장 큰 값을 찾을 때는 n-1번의 비교만 하면 largest key를 찾을 수 있었다.
그럼 그다음 큰 값을 찾기 위해서는 n-1번의 비교를 해서 largeset key를 찾아서 그 key를 뺀 n-1개의 원소들 중에서 다시 largest key를 찾으면 된다. 따라서 n-1+n-2 = 2n-3이 될 것이다.
그럼 여기서 또 우리는 질문을 던져야 한다.
과연 이것이 최선인가? 정답은 아니다.
차대 키를 구하고 싶다. 차대 키는 2번째로 큰 키다. 차대키는 그러면 최대 키 말고는 질 수가 없다. 이 개념을 이용해서 알고리즘을 향상할 수 있을 것이다.
토너먼트의 경우를 생각해보면 랭킹 2등은 랭킹 1등한테만 진다. 그러면 랭킹 2등이 포함된 집단은 즉 랭킹 1등에게 패배한 집단이 될 것이고 그 집단 중에서 가장 큰 key가 차대 키가 될 것이다.
n개의 key가 있다면 largest key에게 패배한 키의 개수는 lg(n)이 될 것이다. (lg(n)은 log 2 (n) 임)
n-1번의 토너먼트가 진행되고 largest key에게 패배한 키의 집단 중에서 가장 큰 원소를 찾는 것은 lgn-1이기 때문에 총 비교 횟수는 n-1+lgn-1 = n+lgn -2가 될 것이다.
Finding the kth-Smallest key
가장 간편한 방법은 정렬해서 k번쨰인 원소를 return 해주면 될 것이고 그에 따른 시간 T(n)=nlgn일 것이다.
quick sort의 partitioning의 방법을 선택하자.
quick sort를 간단하게 설명하자면 pivot을 선정해서 pivot보다 작다면 pivot의 왼쪽, pivot보다 크다면 pivot의 오른쪽으로 정렬한다.
quick sort의 최악의 경우는 이미 정렬되어있는 상태이다.
n-1번 분할, n-2번 분할... 1번 분할이라 W(n)= n(n-1)/2가 될 것이다.
입력이 발생 확률이 동등하다고 가정할 때
-> 모든 k 값은 같은 빈도수로 들어가고, 모두 pivotpoint값은 같은 빈도수로 넘겨진다.
재귀 호출이 없는 경우 : 결과는 n개 존재한다.
만약 입력 크기가 1인 경우 결과가 2개 존재한다.
만약 입력크기가 2인 경우 : 결과가 4개 존재한다.
이러한 관계를 쭉 나열해보면 n에 대한 식으로 표현이 가능하다.
A(n)<A(n-1)+3이라는 식을 얻을 수 있다. (자세한 건 몰라도 될 것 같다.)
A(n)<3n
이렇게 되면 A(n)의 사간 복잡도는 선형 함수의 시간 복잡도를 가진다고 볼 수 있다.
A(n) ∈ θ(n)이 될 것이다.
median을 이용한 방법
퀵 소트 할 때 pivot에 의해서 배열이 정확하게 반으로 나뉜다면 그 경우가 최상의 경우가 될 것이다. 그럼
그 반으로 가르는 pivot을 어떻게 선정하는가?
여기서 median을 사용한다.
그럼 그 median값을 어떻게 구해야 할까?
n을 5의 홀수 배라고 가정하자. 그럼 n개의 키를 n/5그룹으로 나누는데 각 그룹은 5개씩 키를 가지고 있다.
각 그룹에서의 median 값을 구한다. 그때의 비교 횟수는 각 6번일 것이다. 각 그룹에서 구한 median값들 중에서 또 median을 구하면 그게 우리가 원하는 pivotitem이 될 것이다.
무조건 그 pivotitem이 n개의 median값일 수는 없지만, 최대한 가까운 median값으로 선정된다.
미디안들의 미디안 한쪽에 올 수 있는 키의 개수는 7n/10 -3/2이다.
W(n)=22n이므로
W(n) ∈ θ(n)이다. 최악의 경우에도 선형 시간임을 알 수 있다.
선택 문제에 대한 확률적 알고리즘(Probabilistic Algorithm for Selection problem)
알고리즘의 하한을 구할 때 그 알고리즘이 결정적(deterministic)이라고 가정해왔다.
그러나 그 하한이 확률적 알고리즘에도 성립한다는 것도 언급했다.
세 개의 대표적 랜덤 알고리즘
1. 몬테 카를로 알고리즘
- 반드시 맞는 답을 주지는 않는다.
- 오히려 그 답의 추정치를 제공하고 그 추정치가 맞는 답에 가까울 확률은 알 리즘의 사용시간이 증가할수록 커진다.
2. 샤 워드 알고리즘
- 항상 맞는 답을 준다.
- 최악의 경우보다 평균의 경우 훨씬 빠르게 실행되는 결정적 알고리즘에 적합하게 쓰인다.
3. 라스베이거스 알고리즘
- 항상 맞는 답을 준다.
- 하지만 가끔 답을 주지 않음.
이 단원은 이론적으로 너무 어렵다. 무슨 말인지 잘 모르겠다.
'Skils > Algorithm' 카테고리의 다른 글
| [알고리즘] Intractability & NP-Theory (0) | 2022.06.13 |
|---|---|
| [알고리즘 기말예제문제] 홀수피라미드(C++) (0) | 2022.06.12 |
| [알고리즘-C++] - 외판원 순회 문제(Branch & Bound) (1) | 2022.05.31 |
| [알고리즘-C++] 외판원 순회 문제(Dynamic Programming) (0) | 2022.05.29 |
| [알고리즘-C++] 분기한정(Branch & Bound)를 이용한 0-1 배낭 채우기 (1) | 2022.05.28 |
