저번 게시물에서는 외판원 순회 문제를 동적 계획법을 이용해서 풀어보았다.
이번에는 Branch & Bound(분기한정법)을 이용해서 풀 예정이다.
문제의 목표는 동일하게 출발점에서 모든 노드를 각 한 번씩 방문하고 다시 출발점으로 되돌아오는 최소한의 비용을 가지는 경로를 찾는 것이다.
최고 우선 검색을 사용하기 위해서 각 마디의 한계값을 구할 수 있어야 한다.
0-1 배낭 채우기 문제에서는 총무게가 W를 넘지 않도록 하면서 이익을 최대로 하는 게 목표였기 때문에, 주어진 마디에서부터 뻗어나가서 얻을 수 있는 이익의 상한을 계산하였다. 그리고 어떤 마디에서 당시 최대 이익보다 한계값이 큰 경우에 그 마디를 유망하다고 판단했다.
외판원 문제에서는 주어진 마디에서부터 뻗어나가서 얻을 수 있는 여행경로 길이의 하한을 구할 필요가 있다.
그리고 당시 최소경로길이보다 한계값이 작은 경우에 그 마디를 유망하다고 한다.
한계값은 다음과 같이 구한다.
어떤 여행경로라도 그 정점에서 가장 짧은 이음선의 길이들을 선택한 합이 여행경로 길이의 하한일 것이다.
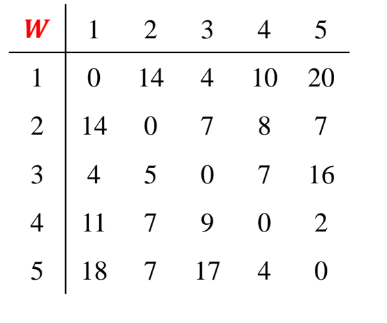
- v1에서 자기 자신을 제외한 가장 짧은 가중치 --> 3
- v2에서 자기 자신을 제외한 가장 짧은 가중치 --> 7
- v3에서 자기 자신을 제외한 가장 짧은 가중치 --> 4
- v4에서 자기 자신을 제외한 가장 짧은 가중치 --> 2
- v5에서 자기 자신을 제외한 가장 짧은 가중치 --> 4
여행경로 길이의 하한값은 21이다.
💡21인 여행경로가 무조건 있다는 뜻은 아니다. 하지만 이 21보다 더 짧은 경로는 있을 수 없다는 뜻이다.
📗V1에서 출발해서 V2를 방문한 경우
- V1->V2의 가중치는 14이다.
- 여기서 V2에서 갈 수 있는 선택지는 자기 자신과 V1을 제외한 모든 곳이다.
- V2=[
14,0,7,8,7] 중에서 가장 작은 값인 7을 선택할 것이다.
- V2=[
- V3, V4, V5는 V2와 자기 자신을 방문하지 못한다.
- V3=[4,
5,0,7,16] 중에서 4를 가진다. - V4=[11,
7,9,0,2] 중에서 2를 가진다. - V5=[18,
7,17,4,0] 중에서 4를 가진다.
- V3=[4,
- 이렇게 된다면 여행경로 길이의 하한은 14+7+4+2+4 = 31이다.
💡이런 식으로 각 방문한 정점들을 빼고 여행경로 길이의 하한을 구해줄 수 있을 것이다.
📕이제 이렇게 구해준 한계값으로 가지치기를 해 볼 것이다.
아래 그림은 각 방문한 정점마다 bound값을 구한 상태이다.
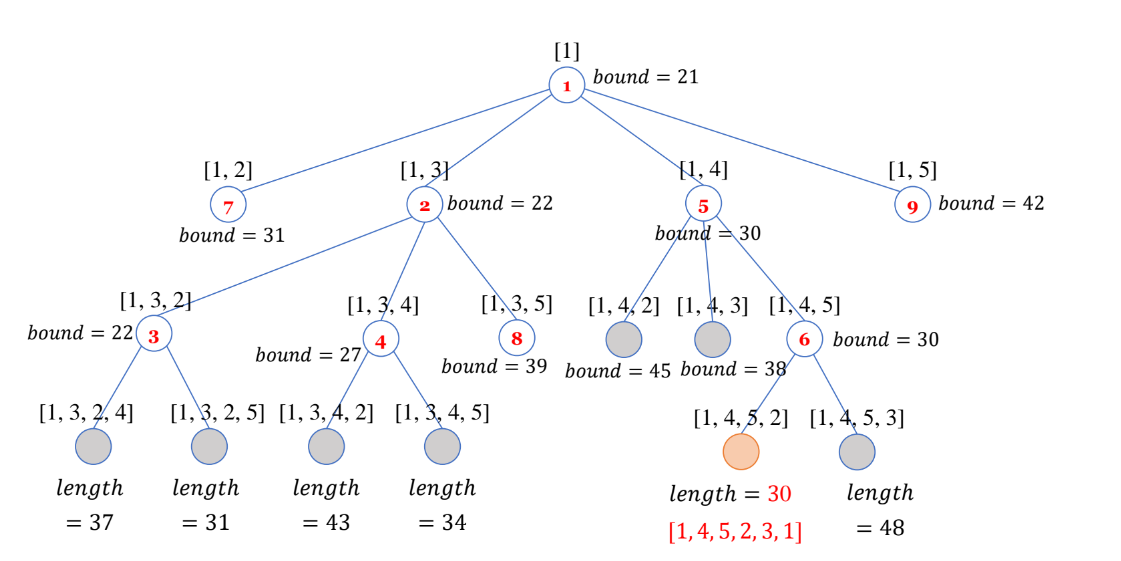
- root를 방문한다.
- bound값을 계산하면 21이 된다.
- root의 자식들을 방문한다.
- [1,2] = 31
- [1,3]=22
- [1,4]=30
- [1,5]=42
- 그중에서 bound값이 가장 작고 확장하지 않은 마디인 [1,3]의 자식 노드들을 방문한다.
- [1,3,2]=22
- [1,3,4]=27
- [1,3,5]=39
- 그 중에서 bound값이 가장 작고 확장하지 않은 마디인 [1,3,2]의 자식노드들을 방문한다.
- 여기서 만약 트리의 깊이가 n-1이라면 길이를 결정해준다.
- [1,3,2,4]를 방문하면 마지막 경로는 자동으로 정해지기 때문에 그다음 깊이를 탐색할 필요 없이 [1,3,2,4,5,1]의 경로 길이를 구해준다.
- [1,3,2,4,5,1]=37
- [1,3,2,5,4,1]=31
- 여기서 구해준 경로의 길이 중에서 가장 작은 것을 minlength로 두고 트리의 bound값이 minlength보다 작은 곳들은 유망하지 않기 때문에 방문에서 제외된다.
- 위 과정을 반복함.
- 결과는 [1,4,5,2,3,1]이 최적 경로가 되고 그 길이의 합은 30이 된다.
외판원 문제를 분기 한정으로 풀면 방문 횟수에서 엄청난 효율성을 보인다.
구현
1.bound값이 작은 것부터 확장해야 하기 때문에 우선순위 큐를 사용해서 bound의 오름차순으로 정렬한다.
struct cmp
{
bool operator()(node_pointer a, node_pointer b) // bound가 작은걸 top으로 두고싶음.
{
return a->bound > b->bound;
}
};
priority_queue<node_pointer, vector<node_pointer>, cmp> pq; // path,bound값으로 나눠야함.2. 구조체 node 설정
typedef struct node *node_pointer;
typedef struct node
{
int level;
vector<int> path;
int bound;
} nodetype;3. 여행경로 길이의 하한을 구하는 Bound함수
int Bound(node_pointer V) //여행길이의 하한을 구하는 함수. 그 하한으로 pq를 구성하고 bound값이 낮은 것을 우선적으로 탐색함.
//만약 모든 도시를 도착한 상황에서 bound는 그 경로의 lenth이다.
{
int lower = length(V->path); //간 경로까지의 길이를 더해줌.
for (int i = 1; i <= G; i++)
{
// i는 내가 출발하는 도시다.
// i에서 다른 도시로 진출한지 안한지를 체크함. 만약 {1,2}라면 1은 제외시키지만 2는 제외를 안시킴.
//왜냐하면 2는 아무 도시로든 edge를 뻗지 않았기때문이다.
if (hasOutgoing(i, V->path)) // true면 내가 이미 경로가 정해졌다. 제외시켜줌.
continue;
int min = INF;
for (int j = 1; j <= G; j++)
{
if (i == j) //자기 자신으로 가는 경우는 제외함.
continue;
if (j == 1 & i == V->path[V->path.size() - 1])
//내가 모든 도시를 방문하지 않은 상황이라고 가정할때 j는 내가 방문할 도시고 i는 내가 출발할 도시이다.
//만약 모든 도시를 방문하지 않은 상황에서 마지막경로에서 1로 가면 안된다. 1(출발점)으로 간다는 것은
//맨 마지막 경우이기때문이다. 그래도 모든 도시를 방문한 상황에서는 출발점으로 돌아가야하는것아니냐?
//라는 의문이 들 수 있는데 모든 도시를 방문한 상황에서는 위의 for문을 돌지않고 바로 bound값은 path의 길이가 된다.
continue;
if (hasIncoming(j, V->path)) // hasIncoming은 내가 밟을 도시를 체크한다. 만약 내가 밟을 도시가 path안에 있다면 그 도시는 제외시켜야함.
continue;
if (min > graph[i][j]) //만약 min값보다 작다면 min값을 넣어줌.
min = graph[i][j];
}
lower += min; // path + min값을 계속 넣어줌. 모든 방문이 끝날떄까지.
}
return lower;
}4. 여행경로의 실제 길이를 구하는 length함수
int length(vector<int> &path) //경로의 길이를 구하는 함수.
{
vector<int>::iterator it;
int len = 0;
for (it = path.begin(); it != path.end(); it++) // path의 경로를 넣고 경로 -> 다음 경로의 길이를 len에 계속 더해줌.
{
if (it != path.end() - 1) //만약 it이 path end-1일 경우 마지막 경로이기 때문에 it+1은 존재하지않는 경로이다.
len += graph[*it][*(it + 1)];
}
return len;
}5. 올 바른 경로인지 검사하는 correct path함수
bool correct_path(node_pointer a) // path에서경로가 없는 경우가 있음.
{
bool flag;
flag = true;
for (int x = 1; x < a->path.size(); x++)
{
if (graph[a->path[x - 1]][a->path[x]] == INF) //경로가 없다면
{
flag = false;
}
}
return flag;
}6. 마지막 경로는 자동으로 정해줘야 하기 때문에 방문 경로를 검사해주는 함수 inIn
bool isIn(int i, vector<int> &path) // path안에 i가 있냐 없냐를 따짐.
{
vector<int>::iterator it;
// cout<<1;
bool opt = true;
for (int j = 0; j <= path.size() - 1; j++)
{
if (i == path[j]) //같은게 있으면
return false;
}
// cout<<"opt는" << opt<<endl;
return true;
}7. 적절한 방문인지 검사하는 함수
bool hasOutgoing(int v, vector<int> &path) // v가 다른 도시를 방문햇느냐?를 찾는것 경로가 2개가 될 수는 없기 떄문에 이미
//경로를 뻗엇다면 그 도시는 제외시켜줘야함. true면 뻗었다는 뜻, false는 뻗지않았다는 뜻.
{
vector<int>::iterator it;
for (it = path.begin(); it != path.end() - 1; it++) //마지막 지점은 1번으로 뻗어야하기때문에 제외시켜줌.
if (*it == v)
return true;
return false;
}
bool hasIncoming(int v, vector<int> &path) // v가 방문된 도시인지 체크함. 두번 방문할 수 없기 떄문에 만약 있다면 true 없다면 false를 return
{
vector<int>::iterator it;
for (it = path.begin() + 1; it != path.end(); it++) //시작지점은 방문은 했지만 한번더 방문해야되기때문에 제외시켜줌.
if (*it == v)
return true;
return false;
}
전체 코드
/*
각 정점에 대한 bound값이 있음. 그 값은 바로 그 정점에서 최소비용으로 갈 수있는 경로의 가중치
그렇게 정점마다 bound값을 뽑아서 다 더 하면 그 값이 여행경로 길이의 하한일것이다.
이 길이의 합과 같은 여행경로가 무조건 있다는 뜻은 아니고 이 보다 더 짧은 경로가 있을 수 없다는 뜻이다.
여행경로의 하한은 이미 뽑힌 값은 제외하고 그 출발지에 따른 bound값이다.
출발지에서 부터 하나씩 방문해서 bound값이 가장 작고 아래까지 탐색을 안한 것ㅂ ㅜ터 탐색함.
*/
#include <iostream>
#include <vector>
#include <algorithm>
#include <queue>
#include <string>
#define INF 999
using namespace std;
int G, v;
vector<vector<int>> graph;
vector<int> bound;
typedef vector<int> ordered_set;
typedef struct node *node_pointer;
typedef struct node
{
int level;
vector<int> path;
int bound;
} nodetype;
int length(vector<int> &path);
int Bound(node_pointer V);
node_pointer create_node(int Level, vector<int> &path);
bool hasIncoming(int v, vector<int> &path);
bool hasOutgoing(int v, vector<int> &path);
void travel2(vector<int> &opttour, int &minlength);
bool isIn(int i, vector<int> &path);
bool correct_path(node_pointer a);
void print(node_pointer a);
vector<int> seq;
int shortpath = INF;
int start = 1;
struct cmp
{
bool operator()(node_pointer a, node_pointer b) // bound가 작은걸 top으로 두고싶음.
{
return a->bound > b->bound;
}
};
int main()
{
cin >> G >> v;
graph.resize(G + 1, vector<int>(G + 1, INF));
bound.resize(G + 1);
for (int i = 0; i < v; i++)
{
int s, f, w;
cin >> s >> f >> w;
graph[s][f] = w;
}
for (int i = 1; i <= G; i++) //인접행렬이기때문에 자기자신은 0으로 초기화함.
{
graph[i][i] = 0;
}
travel2(seq, shortpath);
cout << shortpath << endl;
for (int i = 0; i < seq.size(); i++)
{
if (i < seq.size() - 1)
cout << seq[i] << " ";
else
cout << seq[i];
}
}
int length(vector<int> &path) //경로의 길이를 구하는 함수.
{
vector<int>::iterator it;
int len = 0;
for (it = path.begin(); it != path.end(); it++) // path의 경로를 넣고 경로 -> 다음 경로의 길이를 len에 계속 더해줌.
{
if (it != path.end() - 1) //만약 it이 path end-1일 경우 마지막 경로이기 때문에 it+1은 존재하지않는 경로이다.
len += graph[*it][*(it + 1)];
}
return len;
}
int Bound(node_pointer V) //여행길이의 하한을 구하는 함수. 그 하한으로 pq를 구성하고 bound값이 낮은 것을 우선적으로 탐색함.
//만약 모든 도시를 도착한 상황에서 bound는 그 경로의 lenth이다.
{
int lower = length(V->path); //간 경로까지의 길이를 더해줌.
for (int i = 1; i <= G; i++)
{
// i는 내가 출발하는 도시다.
// i에서 다른 도시로 진출한지 안한지를 체크함. 만약 {1,2}라면 1은 제외시키지만 2는 제외를 안시킴.
//왜냐하면 2는 아무 도시로든 edge를 뻗지 않았기때문이다.
if (hasOutgoing(i, V->path)) // true면 내가 이미 경로가 정해졌다. 제외시켜줌.
continue;
int min = INF;
for (int j = 1; j <= G; j++)
{
if (i == j) //자기 자신으로 가는 경우는 제외함.
continue;
if (j == 1 & i == V->path[V->path.size() - 1])
//내가 모든 도시를 방문하지 않은 상황이라고 가정할때 j는 내가 방문할 도시고 i는 내가 출발할 도시이다.
//만약 모든 도시를 방문하지 않은 상황에서 마지막경로에서 1로 가면 안된다. 1(출발점)으로 간다는 것은
//맨 마지막 경우이기때문이다. 그래도 모든 도시를 방문한 상황에서는 출발점으로 돌아가야하는것아니냐?
//라는 의문이 들 수 있는데 모든 도시를 방문한 상황에서는 위의 for문을 돌지않고 바로 bound값은 path의 길이가 된다.
continue;
if (hasIncoming(j, V->path)) // hasIncoming은 내가 밟을 도시를 체크한다. 만약 내가 밟을 도시가 path안에 있다면 그 도시는 제외시켜야함.
continue;
if (min > graph[i][j]) //만약 min값보다 작다면 min값을 넣어줌.
min = graph[i][j];
}
lower += min; // path + min값을 계속 넣어줌. 모든 방문이 끝날떄까지.
}
return lower;
}
bool hasOutgoing(int v, vector<int> &path) // v가 다른 도시를 방문햇느냐?를 찾는것 경로가 2개가 될 수는 없기 떄문에 이미
//경로를 뻗엇다면 그 도시는 제외시켜줘야함. true면 뻗었다는 뜻, false는 뻗지않았다는 뜻.
{
vector<int>::iterator it;
for (it = path.begin(); it != path.end() - 1; it++) //마지막 지점은 1번으로 뻗어야하기때문에 제외시켜줌.
if (*it == v)
return true;
return false;
}
bool hasIncoming(int v, vector<int> &path) // v가 방문된 도시인지 체크함. 두번 방문할 수 없기 떄문에 만약 있다면 true 없다면 false를 return
{
vector<int>::iterator it;
for (it = path.begin() + 1; it != path.end(); it++) //시작지점은 방문은 했지만 한번더 방문해야되기때문에 제외시켜줌.
if (*it == v)
return true;
return false;
}
void travel2(vector<int> &opttour, int &minlength)
{
priority_queue<node_pointer, vector<node_pointer>, cmp> pq; // path,bound값으로 나눠야함.
node_pointer a, b;
a = (node_pointer)malloc(sizeof(nodetype));
b = (node_pointer)malloc(sizeof(nodetype));
minlength = INF;
b->level = 0;
b->path.push_back(1);
b->bound = Bound(b); //
cout << b->level << " " << b->bound << " ";
print(b);
pq.push(b);
while (!pq.empty())
{
b = pq.top();
pq.pop();
if (b->bound < minlength) // bound값이 minlength보다 작아야 유망하다.
{
// a->level = b->level + 1; // a를 b의 자식노드로 놓음.
for (int i = 2; i <= G; i++)
{
if (isIn(i, b->path) == 0) // isIn값이 0이면 i가 경로에 이미 있다는 소리고 1이면 i가 경로에 없다는 소리다.
{
continue; // 만약 i가 b의 경로에 있다ㅕㅁㄴ?
}
a = create_node(b->level + 1, b->path); //여가서 5일때 터짐.
a->level = b->level + 1;
a->path = b->path;
a->bound = 0;
a->path.push_back(i);
if (a->level == G - 2) // a->level이 도시개수-2개라는 뜻은 마지막경로빼고 다 결정된 상황
//마지막 경로는 굳이 구할필요없이 방문안한 도시를 자동으로 넣어주면 되는것. G-2인 이유는 출발점의 방문은 level이 0이므로
{
for (int k = 1; k <= G; k++) // 1부터 k까지해서 간경로는 재끼고 안간경로를 당연히 가야하므로 푸쉬해줌.
{
if (isIn(k, a->path) == 0) // 0이면 경로 x 1이면 경로 o
{
continue;
}
else
{
a->path.push_back(k);
}
}
a->path.push_back(1); //마지막은 1로 돌아가야함. //1은 start로 바꾸자.
if (length(a->path) < minlength)
{
minlength = length(a->path);
;
opttour.assign(a->path.begin(), a->path.end());
}
a->bound = Bound(a);
if (correct_path(a)) //여기도 경로가 없는거였다면 구분해줘야함. 0이면 없고 1이면 잇음
{
cout << a->level << " " << a->bound << " ";
print(a);
}
else
{
a->bound = Bound(a);
cout << a->level << " "
<< "INF"
<< " ";
print(a);
}
}
else //a->level이 G-2가 아닐때는 직접 다 방문해야함.
{
bool flag = true;
if (correct_path(a)) //path가 적절한가?
{
a->bound = Bound(a);
cout << a->level << " " << a->bound << " ";
print(a);
}
else //이상한 경로라면 INF를 넣어줌.
{
a->bound = Bound(a);
cout << a->level << " "
<< "INF"
<< " ";
print(a);
}
// path가 있는지 없는지 확인 만약 path가 있다면 bound는 bound로 값을 구해주고 아니면 INF를 넣어줌.
if (a->bound < minlength) // bound가 초기화 된 minlength보다 작다면 넣어준다.
pq.push(a);
}
}
}
}
}
bool correct_path(node_pointer a) // 1이면 경로가 있고 0이면 경로가 없다.
{
bool flag;
flag = true;
for (int x = 1; x < a->path.size(); x++)
{
if (graph[a->path[x - 1]][a->path[x]] == INF) //경로가 없다면
{
flag = false;
}
}
return flag;
}
bool isIn(int i, vector<int> &path) // path안에 i가 있냐 없냐를 따짐.
{
vector<int>::iterator it;
// cout<<1;
bool opt = true;
for (int j = 0; j <= path.size() - 1; j++)
{
if (i == path[j]) //같은게 있으면
return false;
}
// cout<<"opt는" << opt<<endl;
return true;
}
node_pointer create_node(int Level, vector<int> &path)
{
node_pointer temp = (node_pointer)malloc(sizeof(node) * G);
// temp->level=Level+1;
// temp->path=path;
// temp->bound=0;
return temp;
}
void print(node_pointer a)
{
for (int x = 0; x < a->path.size(); x++)
{
if (x < a->path.size() - 1)
cout << a->path[x] << " ";
else
cout << a->path[x];
}
cout << endl;
}'Skils > Algorithm' 카테고리의 다른 글
| [알고리즘 기말예제문제] 홀수피라미드(C++) (0) | 2022.06.12 |
|---|---|
| [알고리즘-C++] 계산복잡도 (0) | 2022.05.31 |
| [알고리즘-C++] 외판원 순회 문제(Dynamic Programming) (0) | 2022.05.29 |
| [알고리즘-C++] 분기한정(Branch & Bound)를 이용한 0-1 배낭 채우기 (1) | 2022.05.28 |
| [C++] 알고리즘 이론 - Branch & Bound (분기 한정) (0) | 2022.05.28 |
