💡데이터의 종류
- 특성에 따른 분류
범주형(Categorical Data): 산술 연산이 불가능함-> 도수분포표 table() 함수를 이용(남/녀, 혈액형 등 값의 범위가 있음)연속형(수치형, Numerical Data): 수치로 측정되기 때문에 산술 연산 가능 (시험성적,몸무게,키 등)
- 변수 개수에 의한 분류
일변량(Unvariable Data): 변수 개수가 한 개 ->Vector 사용다변량(Multivariable Data): 변수 개수가 두개 이상 -> Matrix or Data.Frame 이용이변량(Bivariable): 변수 개수가 두개 ex) '키'가 크면 '몸무게'도 많이 나간다.
👀이변량 데이터 정리
📗범주형자료의 이원 분할표

x=rbind(c(54,7),c(3,12))
rownames(x)=c("부모착용","부모미착용")
colnames(x)=c("아이착용","아이미착용")
margin.table(x,1)
margin.table(x,2)
addmargins(x)
prop.table(x)
조금 깔끔하게 행, 열 맞게 출력하고 싶은데 그게 잘 안 되는 것 같다. R은 참 불편한 게 많네..
아무튼 위의 그림처럼 테이블을 만들었다.
barplot(x,main="벨트착용유무",legend.text=T) ##legend.text=색깔이 뭘 의미하는지 명시해줌. default는 F
barplot(x,main="벨트착용유무",legend.text=F)
barplot(x,main="벨트착용유무",legend.text=T,beside=T) ##beside는 bar끼리 분리함. default는 F
barplot(x,main="벨트착용유무",legend.text=T,beside=F)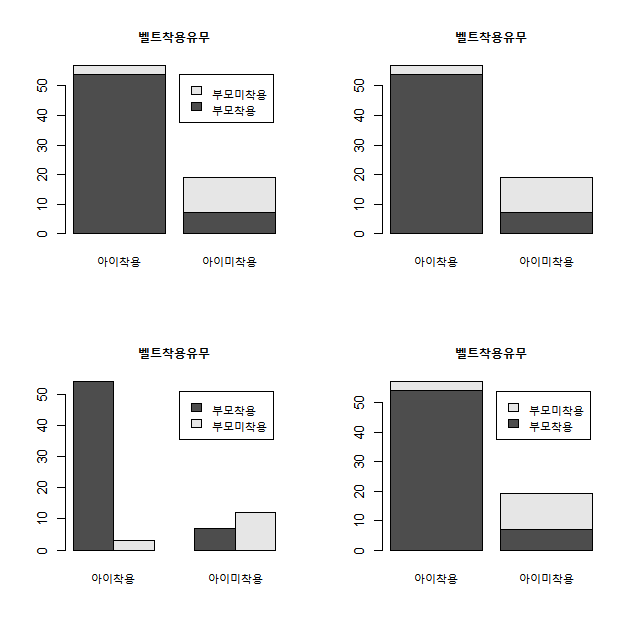
👀상관계수(양적 자료)
: 두 변수 사이의 통계적 관계를 표현하기 위해 특정한상관관계의 정도를 수치적으로 나타낸 계수이다.
machine = c(68,82,94,106,92,80,76,74,110,93,86,65,74,84,100)
expert= c(72,84,89,100,97,88,84,70,103,84,86,63,69,87,93)
plot(machine,expert) ## 산점도, machine과 expert의 관계가 궁금함.
산점도는 직교 좌표계(도표)를 이용해 좌표상의 점들을 표시함으로써 두 개 변수 간의 관계를 나타내는 그래프 방법이다. 도표 위에 두 변수 X와 Y값이 만나는 지점을 표시한 그림. 이 그림을 통해 두 변수 사이의 관계를 알 수 있다.
📕상관관계
산점 도내에서 파악할 수 있는 패턴이나 관계를 의미합니다.
상관관계는 데이터에 관련성이 있는지를 설명해준다.
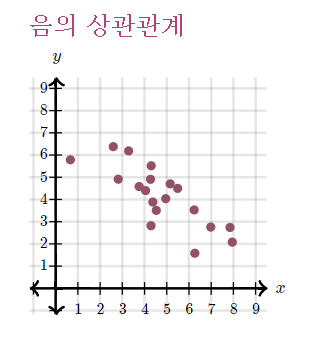
- 음의 상관관계
- x값이 증가할 때 y값이 감소한다면 두 데이터는
음의 상관관계라고 말합니다.
- x값이 증가할 때 y값이 감소한다면 두 데이터는
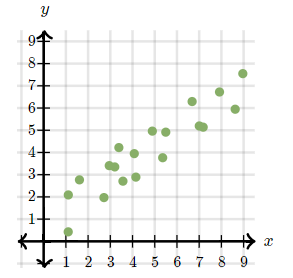
- 양의 상관 관계
- x값이 증가할 때 y값도 증가한다면 두 데이터는
양의 상관관계라고 말합니다.
- x값이 증가할 때 y값도 증가한다면 두 데이터는
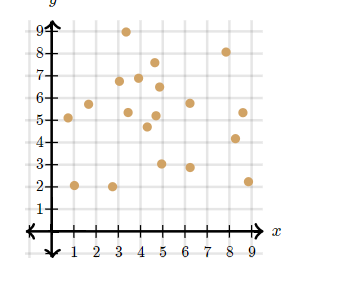
- 상관 관계없음
- 두 데이터 간의 어떠한 패턴이 발견되지 않는 관계를 말합니다.
📕상관 계수
변수 간의 관계의 정도와 방향을 하나의 수치로 요약해주는 지수다.
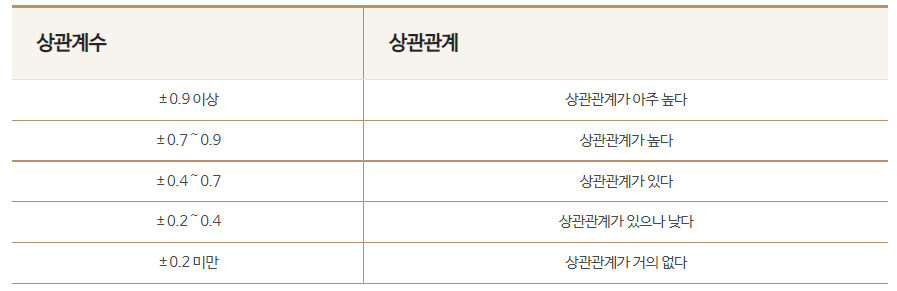
📕상관계수의 종류 (일반적으로 상관계수라 함은 Pearson's의 상관계수를 의미한다.)
📗Pearson's 상관 계수

cor(machine,expert) ##일반적으로 상관계수는 `Pearson's 상관계수`를 의미한다.
machine과 expert의 상관계수는 0.9로 상관관계가 아주 높다고 판단할 수 있다.
r1=cov(machine,expert)/(sd(machine)*sd(expert)) ## R프로그래밍을 이용한 Pearson's 상관계수 계산x=machine;y=expert
xbar=mean(x); ybar=mean(y)
sum1=0; sum2=0; sum3=0
for( i in 1 : length(x)){
sum1=sum1+(x[i]-xbar)^2
sum2=sum2+(y[i]-ybar)^2
sum3= sum3+(x[i]-xbar)*(y[i]-ybar)
}
r2=sum3/sqrt(sum1*sum2)cor(machine,expert,method="spearman") ##Spearman's 상관계수모두 다 Pearson's 상관계수를 구하는 방법이다.
📗Spearman's 상관계수

machine과 expert의 Spearman's 상관계수는 0.88로 상관관계가 높다고 판단할 수 있다.
'학교 > R프로그래밍' 카테고리의 다른 글
| R프로그래밍 기말고사정리 07 - 통계적 가설 검정 (0) | 2022.06.05 |
|---|---|
| R프로그래밍 기말고사정리06- 일표본 유의성 검정 (0) | 2022.06.05 |
| R프로그래밍 기말고사 정리 04 - 연속확률분포에서의 중심극한정리 (0) | 2022.06.05 |
| R프로그래밍 기말고사 정리 -03 이산확률분포에서의 중심극한정리 (0) | 2022.06.05 |
| R프로그래밍 기말고사 정리 -02 중심극한정리 (0) | 2022.06.04 |
💡데이터의 종류
- 특성에 따른 분류
범주형(Categorical Data): 산술 연산이 불가능함-> 도수분포표 table() 함수를 이용(남/녀, 혈액형 등 값의 범위가 있음)연속형(수치형, Numerical Data): 수치로 측정되기 때문에 산술 연산 가능 (시험성적,몸무게,키 등)
- 변수 개수에 의한 분류
일변량(Unvariable Data): 변수 개수가 한 개 ->Vector 사용다변량(Multivariable Data): 변수 개수가 두개 이상 -> Matrix or Data.Frame 이용이변량(Bivariable): 변수 개수가 두개 ex) '키'가 크면 '몸무게'도 많이 나간다.
👀이변량 데이터 정리
📗범주형자료의 이원 분할표

x=rbind(c(54,7),c(3,12)) rownames(x)=c("부모착용","부모미착용") colnames(x)=c("아이착용","아이미착용") margin.table(x,1) margin.table(x,2) addmargins(x) prop.table(x)

조금 깔끔하게 행, 열 맞게 출력하고 싶은데 그게 잘 안 되는 것 같다. R은 참 불편한 게 많네..
아무튼 위의 그림처럼 테이블을 만들었다.
barplot(x,main="벨트착용유무",legend.text=T) ##legend.text=색깔이 뭘 의미하는지 명시해줌. default는 F barplot(x,main="벨트착용유무",legend.text=F) barplot(x,main="벨트착용유무",legend.text=T,beside=T) ##beside는 bar끼리 분리함. default는 F barplot(x,main="벨트착용유무",legend.text=T,beside=F)

👀상관계수(양적 자료)
: 두 변수 사이의 통계적 관계를 표현하기 위해 특정한상관관계의 정도를 수치적으로 나타낸 계수이다.
machine = c(68,82,94,106,92,80,76,74,110,93,86,65,74,84,100) expert= c(72,84,89,100,97,88,84,70,103,84,86,63,69,87,93) plot(machine,expert) ## 산점도, machine과 expert의 관계가 궁금함.

산점도는 직교 좌표계(도표)를 이용해 좌표상의 점들을 표시함으로써 두 개 변수 간의 관계를 나타내는 그래프 방법이다. 도표 위에 두 변수 X와 Y값이 만나는 지점을 표시한 그림. 이 그림을 통해 두 변수 사이의 관계를 알 수 있다.
📕상관관계
산점 도내에서 파악할 수 있는 패턴이나 관계를 의미합니다.
상관관계는 데이터에 관련성이 있는지를 설명해준다.
- 음의 상관관계
- x값이 증가할 때 y값이 감소한다면 두 데이터는
음의 상관관계라고 말합니다.
- x값이 증가할 때 y값이 감소한다면 두 데이터는

- 양의 상관 관계
- x값이 증가할 때 y값도 증가한다면 두 데이터는
양의 상관관계라고 말합니다.
- x값이 증가할 때 y값도 증가한다면 두 데이터는

- 상관 관계없음
- 두 데이터 간의 어떠한 패턴이 발견되지 않는 관계를 말합니다.

📕상관 계수
변수 간의 관계의 정도와 방향을 하나의 수치로 요약해주는 지수다.

📕상관계수의 종류 (일반적으로 상관계수라 함은 Pearson's의 상관계수를 의미한다.)
📗Pearson's 상관 계수

cor(machine,expert) ##일반적으로 상관계수는 `Pearson's 상관계수`를 의미한다.
machine과 expert의 상관계수는 0.9로 상관관계가 아주 높다고 판단할 수 있다.
r1=cov(machine,expert)/(sd(machine)*sd(expert)) ## R프로그래밍을 이용한 Pearson's 상관계수 계산x=machine;y=expert xbar=mean(x); ybar=mean(y) sum1=0; sum2=0; sum3=0 for( i in 1 : length(x)){ sum1=sum1+(x[i]-xbar)^2 sum2=sum2+(y[i]-ybar)^2 sum3= sum3+(x[i]-xbar)*(y[i]-ybar) } r2=sum3/sqrt(sum1*sum2)
cor(machine,expert,method="spearman") ##Spearman's 상관계수모두 다 Pearson's 상관계수를 구하는 방법이다.
📗Spearman's 상관계수

machine과 expert의 Spearman's 상관계수는 0.88로 상관관계가 높다고 판단할 수 있다.
'학교 > R프로그래밍' 카테고리의 다른 글
| R프로그래밍 기말고사정리 07 - 통계적 가설 검정 (0) | 2022.06.05 |
|---|---|
| R프로그래밍 기말고사정리06- 일표본 유의성 검정 (0) | 2022.06.05 |
| R프로그래밍 기말고사 정리 04 - 연속확률분포에서의 중심극한정리 (0) | 2022.06.05 |
| R프로그래밍 기말고사 정리 -03 이산확률분포에서의 중심극한정리 (0) | 2022.06.05 |
| R프로그래밍 기말고사 정리 -02 중심극한정리 (0) | 2022.06.04 |
