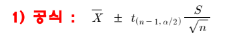💡모평균의 신뢰구간
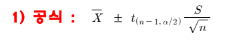
신뢰구간이 u를 포함학 확률이 (1-α)*100 % dp 가까운지 확인
📕정규분포
모집단이 정규분포인 경우 모평균에 대한 신뢰구간의 신뢰도 비교 시뮬레이션
입력값 : 모평균(mu), 모표준편차(sd), 표본의 크기(n), 자료 set의 크기(m), 신뢰도(alpha)
📗입력
mu=0; sd=1;n=5;m=100000;alpha=0.95📗크기
mu=0; sd=1;m=100000;alpha=0.95
n=c(5,10,15,20)
count=0
a=alpha+(1-alpha)/2
for(j in 1 : length(n)){
for(i in 1 : m){
x=rnorm(n[j],mu,sd)
xbar=mean(x)
se=sd(x)/sqrt(n[j])
L=xbar-qt(a,n[j]-1)*se
U=xbar+qt(a,n[j]-1)*se
if(mu>=L && mu<=U)count=count+1
}
P=count/m*100
cat("표본의 수 = ",n[j],"포함확률 = ",P,"\n")
count=0
}
정규분포는 m이 충분히 큰 상황일때 n이 작아도 95%로 빠르게 다가간다.
📕지수분포
모집단이 지수 분포인 경우 모평균에 대한 신뢰구간의 신뢰도 비교 시물레이션
입력값 : 자유도(r), 표본의 크기(n), 자료 set의 크기(m), 신뢰도(alpha)
📗입력
r=1; n=5; m=100000; alpha=0.95📗코드
r=1;m=100000; alpha=0.95
mu=1/r
count=0
a=alpha+(1-alpha)/2
for(j in 1 : length(n)){
for(i in 1 : m){
x=rexp(n[j],rate=r)
xbar=mean(x)
se=sd(x)/sqrt(n[j])
L=xbar-qt(a,n[j]-1)*se
U=xbar+qt(a,n[j]-1)*se
if(mu>=L && mu<=U) count=count+1
}
P=count/m*100
cat("표본의 수 = ",n[j],"포함확률 = ",P,"\n")
count=0
}
📗결과

지수 분포도 n이 커질수록 95%를 포함하지만 정규분포보다 속도가 느리다.
📕포아송 분포
📗입력
lambda=5; n=5; m=100000;alpha=0.95📗코드
lambda=5;m=100000;alpha=0.95
mu=lambda; count=0
a=alpha+(1-alpha)/2
for(j in 1 : length(n)){
for(i in 1 : m){
x=rpois(n[j],lambda)
xbar=mean(x)
se=sd(x)/sqrt(n[j])
L=xbar-qt(a,n-1)*se
U=xbar+qt(a,n-1)*se
if(mu>=L && mu<=U)count=count+1
}
P=count/m*100
cat(" 표본의 수=",n," 포함확률 = ",P,"\n")
count=0
}📗결과

포아송 분포도 m이 충분히 큰 상황에서 표본의 크기가 커짐에 따라 95%까지 도달했다.
정규분포> 포아송> 지수 분포 순으로 95%에 도달했다.
'학교 > R프로그래밍' 카테고리의 다른 글
| R프로그래밍 기말고사 정리 12- 이표본 모비율차 검정(prop.test) (0) | 2022.06.13 |
|---|---|
| R프로그래밍 기말고사 정리 10 - 이표본 검정(이변량데이터) (0) | 2022.06.13 |
| R프로그래밍 기말고사정리 09- 이표본 검정 (0) | 2022.06.13 |
| R프로그래밍 기말고사 정리 08 - 이표본비율 (0) | 2022.06.13 |
| R프로그래밍 기말고사정리 07 - 통계적 가설 검정 (0) | 2022.06.05 |
💡모평균의 신뢰구간
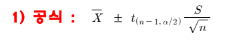
신뢰구간이 u를 포함학 확률이 (1-α)*100 % dp 가까운지 확인
📕정규분포
모집단이 정규분포인 경우 모평균에 대한 신뢰구간의 신뢰도 비교 시뮬레이션
입력값 : 모평균(mu), 모표준편차(sd), 표본의 크기(n), 자료 set의 크기(m), 신뢰도(alpha)
📗입력
mu=0; sd=1;n=5;m=100000;alpha=0.95📗크기
mu=0; sd=1;m=100000;alpha=0.95 n=c(5,10,15,20) count=0 a=alpha+(1-alpha)/2 for(j in 1 : length(n)){ for(i in 1 : m){ x=rnorm(n[j],mu,sd) xbar=mean(x) se=sd(x)/sqrt(n[j]) L=xbar-qt(a,n[j]-1)*se U=xbar+qt(a,n[j]-1)*se if(mu>=L && mu<=U)count=count+1 } P=count/m*100 cat("표본의 수 = ",n[j],"포함확률 = ",P,"\n") count=0 }

정규분포는 m이 충분히 큰 상황일때 n이 작아도 95%로 빠르게 다가간다.
📕지수분포
모집단이 지수 분포인 경우 모평균에 대한 신뢰구간의 신뢰도 비교 시물레이션
입력값 : 자유도(r), 표본의 크기(n), 자료 set의 크기(m), 신뢰도(alpha)
📗입력
r=1; n=5; m=100000; alpha=0.95📗코드
r=1;m=100000; alpha=0.95 mu=1/r count=0 a=alpha+(1-alpha)/2 for(j in 1 : length(n)){ for(i in 1 : m){ x=rexp(n[j],rate=r) xbar=mean(x) se=sd(x)/sqrt(n[j]) L=xbar-qt(a,n[j]-1)*se U=xbar+qt(a,n[j]-1)*se if(mu>=L && mu<=U) count=count+1 } P=count/m*100 cat("표본의 수 = ",n[j],"포함확률 = ",P,"\n") count=0 }
📗결과

지수 분포도 n이 커질수록 95%를 포함하지만 정규분포보다 속도가 느리다.
📕포아송 분포
📗입력
lambda=5; n=5; m=100000;alpha=0.95📗코드
lambda=5;m=100000;alpha=0.95 mu=lambda; count=0 a=alpha+(1-alpha)/2 for(j in 1 : length(n)){ for(i in 1 : m){ x=rpois(n[j],lambda) xbar=mean(x) se=sd(x)/sqrt(n[j]) L=xbar-qt(a,n-1)*se U=xbar+qt(a,n-1)*se if(mu>=L && mu<=U)count=count+1 } P=count/m*100 cat(" 표본의 수=",n," 포함확률 = ",P,"\n") count=0 }
📗결과

포아송 분포도 m이 충분히 큰 상황에서 표본의 크기가 커짐에 따라 95%까지 도달했다.
정규분포> 포아송> 지수 분포 순으로 95%에 도달했다.
'학교 > R프로그래밍' 카테고리의 다른 글
| R프로그래밍 기말고사 정리 12- 이표본 모비율차 검정(prop.test) (0) | 2022.06.13 |
|---|---|
| R프로그래밍 기말고사 정리 10 - 이표본 검정(이변량데이터) (0) | 2022.06.13 |
| R프로그래밍 기말고사정리 09- 이표본 검정 (0) | 2022.06.13 |
| R프로그래밍 기말고사 정리 08 - 이표본비율 (0) | 2022.06.13 |
| R프로그래밍 기말고사정리 07 - 통계적 가설 검정 (0) | 2022.06.05 |