목차
이변량 데이터 : 변수가 두 개인 것 ex) 성별에 따른 키
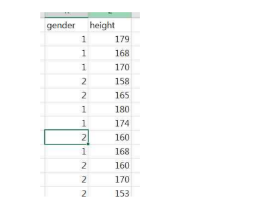
다음 자료는 성별에 따른 키 이다. 남자가 1이고 여자가 2이다.
이러한 자료들은 이표본 검정할 것이다.
아래 자료는 방법 1, 방법 2에 따른 질소성분 함량이다. (등분산이라고 가정)
method=c(1,1,1,1,1,2,2,2,2)
x=c(19.1,32.8,27.6,25.9,28.5,17.0,16.4,16.8,15.5)
t.test(x~method,var.equal=T)

💡해석
- 추정 : 방법 1의 평균 질소성분 함유량은 26.78, 방법2의 평균 질소성분함유량은 16.46이며, 방법1과 방법2의 평균 질소성분함유량에 대한 95%신뢰구간은 (4.33,16.37)이다.
- 가설 검정
- 가설
- H0 : 방법 1과 방법 2의 평균 질소 성분함유량은 같다. [귀무가설]
- H1 : 방법1과 방법2의 평균 질소 성분함유량은 다르다. [대립가설]
- 유의수준 α =0.05
- 검정통계량 T값 =4.0647
- P값 = 0.0047 < α => 귀무가설을 기각, 대립가설 채택
- 결론 : 유의수준 95%에서 방법1과 방법2의 평균 질소 성분함유량은 다르다고 할 수 있다. 방법1의 평균 질소 성분 함유량이 방법2의 평균 질소 성분함유량보다 크다고 할 수있다.
- 가설
📕방법 1과 방법 2의 이표본 분산 검정

💡해석 :
- 가설검정
- 가설
- H0 : 방법1과 방법2의 분산은 같다. [귀무가설]
- H1 : 방법1과 방법2의 분산은 다르다. [대립 가설]
- 유의 수준 α =0.05
- 검정 통계량 F =56.287
- P-value = 0.00748 < α -- > 귀무가설 기각, 대립 가설 채택
- 결론 : 유의 수준 5%에서 방법 1과 방법 2의 분산은 다르다고 할 수 있다. (방법 1과 방법 2는 이분산임)
- 가설
📗R프로그래밍을 이용한 이 표본 분산비 검정 및 이표본 평균 차 검정
T_test_2b = function(data,group){
x=rep(0,length(group))
y=rep(0,length(group))
for( i in 1 : length(group)){
if(group[i]<2) x[i]=data[i]
else y[i]=data[i]
}
x=x[x>0.01]; y=y[y>0.01]
n1=length(x); n2=length(y)
s1=var(x); s2=var(y)
F=s1/s2
pvalue=min(2*pf(F,n1-1,n2-1), 2*(1-pf(F,n1-1,n2-1)))
cat("============= 이표본 분산비 검정==============","\n","\n")
cat(" F=",F,"Pvalue=",pvalue,"\n","\n")
xbar=mean(x);ybar=mean(y)
sp=sqrt(((n1-1)*s1+(n2-1)*s2)/(n1+n2-2))
T=(xbar-ybar)/(sp*sqrt(1/n1+1/n2))
pvalue = 2*(1-pt(abs(T),n1+n2-2))
cat(" ============= 이표본 평균차 검정 ============","\n","\n")
cat(" 등분산인 경우 : T = ",T,"Pvalue= ",pvalue,"\n")
df=(s1/n1+s2/n2)^2/((s1/n1)^2/(n1-1)+(s2/n2)^2/(n2-1))
T=(xbar-ybar)/sqrt(s1/n1+s2/n2)
pvalue=2*(1-pt(abs(T),df))
cat(" 이분산인 경우 : T = ",T,"Pvalue=",pvalue,"\n")
}
method=c(1,1,1,1,1,2,2,2,2)
x=c(19.1,32.8,27.6,25.9,28.5,17.0,16.4,16.8,15.5)
T_test_2b(x,method)실행결과
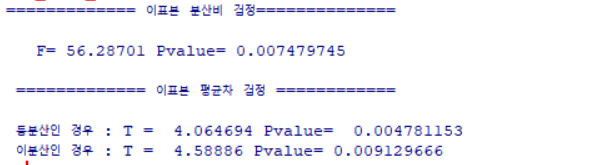
var.test(A~B) --> A를 B로 묶는다
📗연습문제 1
성별에 따라 몸무게에 차이가 있는지 검정하시오.
📕이 표본 분산 검정
var.test(weight~gender)
💡해석
- 가설검정
- 가설
- H0 : 남자와 여자의 몸무게 분산은 같다. [ 귀무가설]
- H1 : 남자와 여자의 몸무게 분산은 다르다. [대립 가설]
- 유의 수준 α = 0.05
- 검정 통계량 F = 1.2463
- P-value = 0.5198 > α => 귀무가설 채택
- 결론 : 유의 수준 5%에서 남자와 여자의 몸무게의 분산은 통계적으로 유의한 차이가 없다.
- 가설
📕분산 검정을 통한 이 표본 평균 차 검정
t.test(weight~gender,var.equal=T)
💡해석
- 추정 : 남자의 몸무게 평균은 77kg이며 , 여자의 몸무게 평균은 56kg이다. 남자와 여자의 평균 몸무게 차이에 대한 95% 신뢰구간은 (17.3, 24.4)이다.
- 가설검정
- 가설
- H0 : 남자와 여자의 몸무게 평균은 같다. [귀무가설]
- H1 : 남자와 여자의 몸무게 평균은 다르다. [대립 가설]
- 유의 수준 α =0.05
- 검정 통계량 T= 11.652
- P-value <α => 귀무가설 기각, 대립 가설 채택
- 결론 : 유의 수준 5%에서 남자의 몸무게 평균과 여자의 몸무게 평균은 같다고 할 수없다. 남자의 평균 몸무게(77kg)가 여자의 평균 몸무게(56kg) 보다 무겁다고 할 수 있다.
- 가설
📗연습문제 2
성별에 따라 bmi에 차이가 있는지 검정하시오.
📕이 표본 분산 검정
var.test(bmi~gender)
💡해석
- 가설검정
- 가설
- H0 : 남자의 분산과 여자의 분산은 같다. [귀무가설]
- H1 : 남자의 분산과 여자의 분산은 다르다. [대립 가설]
- 유의 수준 α =0.05
- 검정 통계량 F=0.83414
- P-value = 0.6059 > α => 귀무가설 채택
- 결론 : 유의 수준 5%에서 남자와 여자의 분산은 통계적으로 유의미한 차이가 없다. (등분산이다.)
- 가설
📕이 표본 평균 차 검정
t.test(bmi~gender,var.equal=T)
💡해석
- 추정
- 남자의 bmi 평균은 24.63이며 여자의 bmi 평균은 21.04이다. 남자와 여자의 평균 bmi에 대한 95% 신뢰구간은 (2.698,4.471)이다.
- 가설검정
- 가설
- H0 : 남자와 여자의 bmi 평균은 같다. [귀무가설]
- H1 : 남자와 여자의 bmi 평균은 다르다. [대립 가설]
- 유의 수준 α =0.05
- 검정 통계량 = 8.06
- P-value < α => 귀무가설 기각, 대립 가설 채택
- 결론 : 유의 수준 5%에서 남자와 여자의 bmi는 다르다고 할 수 있다. 남자의 bmi지수(24.63)이 여자의 bmi지수(21.044)보다 높다고 할 수있다.
- 가설
'학교 > R프로그래밍' 카테고리의 다른 글
| R프로그래밍 기말고사 정리 13 - 모평균의 신뢰구간 (0) | 2022.06.14 |
|---|---|
| R프로그래밍 기말고사 정리 12- 이표본 모비율차 검정(prop.test) (0) | 2022.06.13 |
| R프로그래밍 기말고사정리 09- 이표본 검정 (0) | 2022.06.13 |
| R프로그래밍 기말고사 정리 08 - 이표본비율 (0) | 2022.06.13 |
| R프로그래밍 기말고사정리 07 - 통계적 가설 검정 (0) | 2022.06.05 |
이변량 데이터 : 변수가 두 개인 것 ex) 성별에 따른 키

다음 자료는 성별에 따른 키 이다. 남자가 1이고 여자가 2이다.
이러한 자료들은 이표본 검정할 것이다.
아래 자료는 방법 1, 방법 2에 따른 질소성분 함량이다. (등분산이라고 가정)
method=c(1,1,1,1,1,2,2,2,2) x=c(19.1,32.8,27.6,25.9,28.5,17.0,16.4,16.8,15.5) t.test(x~method,var.equal=T)

💡해석
- 추정 : 방법 1의 평균 질소성분 함유량은 26.78, 방법2의 평균 질소성분함유량은 16.46이며, 방법1과 방법2의 평균 질소성분함유량에 대한 95%신뢰구간은 (4.33,16.37)이다.
- 가설 검정
- 가설
- H0 : 방법 1과 방법 2의 평균 질소 성분함유량은 같다. [귀무가설]
- H1 : 방법1과 방법2의 평균 질소 성분함유량은 다르다. [대립가설]
- 유의수준 α =0.05
- 검정통계량 T값 =4.0647
- P값 = 0.0047 < α => 귀무가설을 기각, 대립가설 채택
- 결론 : 유의수준 95%에서 방법1과 방법2의 평균 질소 성분함유량은 다르다고 할 수 있다. 방법1의 평균 질소 성분 함유량이 방법2의 평균 질소 성분함유량보다 크다고 할 수있다.
- 가설
📕방법 1과 방법 2의 이표본 분산 검정

💡해석 :
- 가설검정
- 가설
- H0 : 방법1과 방법2의 분산은 같다. [귀무가설]
- H1 : 방법1과 방법2의 분산은 다르다. [대립 가설]
- 유의 수준 α =0.05
- 검정 통계량 F =56.287
- P-value = 0.00748 < α -- > 귀무가설 기각, 대립 가설 채택
- 결론 : 유의 수준 5%에서 방법 1과 방법 2의 분산은 다르다고 할 수 있다. (방법 1과 방법 2는 이분산임)
- 가설
📗R프로그래밍을 이용한 이 표본 분산비 검정 및 이표본 평균 차 검정
T_test_2b = function(data,group){ x=rep(0,length(group)) y=rep(0,length(group)) for( i in 1 : length(group)){ if(group[i]<2) x[i]=data[i] else y[i]=data[i] } x=x[x>0.01]; y=y[y>0.01] n1=length(x); n2=length(y) s1=var(x); s2=var(y) F=s1/s2 pvalue=min(2*pf(F,n1-1,n2-1), 2*(1-pf(F,n1-1,n2-1))) cat("============= 이표본 분산비 검정==============","\n","\n") cat(" F=",F,"Pvalue=",pvalue,"\n","\n") xbar=mean(x);ybar=mean(y) sp=sqrt(((n1-1)*s1+(n2-1)*s2)/(n1+n2-2)) T=(xbar-ybar)/(sp*sqrt(1/n1+1/n2)) pvalue = 2*(1-pt(abs(T),n1+n2-2)) cat(" ============= 이표본 평균차 검정 ============","\n","\n") cat(" 등분산인 경우 : T = ",T,"Pvalue= ",pvalue,"\n") df=(s1/n1+s2/n2)^2/((s1/n1)^2/(n1-1)+(s2/n2)^2/(n2-1)) T=(xbar-ybar)/sqrt(s1/n1+s2/n2) pvalue=2*(1-pt(abs(T),df)) cat(" 이분산인 경우 : T = ",T,"Pvalue=",pvalue,"\n") } method=c(1,1,1,1,1,2,2,2,2) x=c(19.1,32.8,27.6,25.9,28.5,17.0,16.4,16.8,15.5) T_test_2b(x,method)
실행결과

var.test(A~B) --> A를 B로 묶는다
📗연습문제 1
성별에 따라 몸무게에 차이가 있는지 검정하시오.
📕이 표본 분산 검정
var.test(weight~gender)
💡해석
- 가설검정
- 가설
- H0 : 남자와 여자의 몸무게 분산은 같다. [ 귀무가설]
- H1 : 남자와 여자의 몸무게 분산은 다르다. [대립 가설]
- 유의 수준 α = 0.05
- 검정 통계량 F = 1.2463
- P-value = 0.5198 > α => 귀무가설 채택
- 결론 : 유의 수준 5%에서 남자와 여자의 몸무게의 분산은 통계적으로 유의한 차이가 없다.
- 가설
📕분산 검정을 통한 이 표본 평균 차 검정
t.test(weight~gender,var.equal=T)
💡해석
- 추정 : 남자의 몸무게 평균은 77kg이며 , 여자의 몸무게 평균은 56kg이다. 남자와 여자의 평균 몸무게 차이에 대한 95% 신뢰구간은 (17.3, 24.4)이다.
- 가설검정
- 가설
- H0 : 남자와 여자의 몸무게 평균은 같다. [귀무가설]
- H1 : 남자와 여자의 몸무게 평균은 다르다. [대립 가설]
- 유의 수준 α =0.05
- 검정 통계량 T= 11.652
- P-value <α => 귀무가설 기각, 대립 가설 채택
- 결론 : 유의 수준 5%에서 남자의 몸무게 평균과 여자의 몸무게 평균은 같다고 할 수없다. 남자의 평균 몸무게(77kg)가 여자의 평균 몸무게(56kg) 보다 무겁다고 할 수 있다.
- 가설
📗연습문제 2
성별에 따라 bmi에 차이가 있는지 검정하시오.
📕이 표본 분산 검정
var.test(bmi~gender)
💡해석
- 가설검정
- 가설
- H0 : 남자의 분산과 여자의 분산은 같다. [귀무가설]
- H1 : 남자의 분산과 여자의 분산은 다르다. [대립 가설]
- 유의 수준 α =0.05
- 검정 통계량 F=0.83414
- P-value = 0.6059 > α => 귀무가설 채택
- 결론 : 유의 수준 5%에서 남자와 여자의 분산은 통계적으로 유의미한 차이가 없다. (등분산이다.)
- 가설
📕이 표본 평균 차 검정
t.test(bmi~gender,var.equal=T)
💡해석
- 추정
- 남자의 bmi 평균은 24.63이며 여자의 bmi 평균은 21.04이다. 남자와 여자의 평균 bmi에 대한 95% 신뢰구간은 (2.698,4.471)이다.
- 가설검정
- 가설
- H0 : 남자와 여자의 bmi 평균은 같다. [귀무가설]
- H1 : 남자와 여자의 bmi 평균은 다르다. [대립 가설]
- 유의 수준 α =0.05
- 검정 통계량 = 8.06
- P-value < α => 귀무가설 기각, 대립 가설 채택
- 결론 : 유의 수준 5%에서 남자와 여자의 bmi는 다르다고 할 수 있다. 남자의 bmi지수(24.63)이 여자의 bmi지수(21.044)보다 높다고 할 수있다.
- 가설
'학교 > R프로그래밍' 카테고리의 다른 글
| R프로그래밍 기말고사 정리 13 - 모평균의 신뢰구간 (0) | 2022.06.14 |
|---|---|
| R프로그래밍 기말고사 정리 12- 이표본 모비율차 검정(prop.test) (0) | 2022.06.13 |
| R프로그래밍 기말고사정리 09- 이표본 검정 (0) | 2022.06.13 |
| R프로그래밍 기말고사 정리 08 - 이표본비율 (0) | 2022.06.13 |
| R프로그래밍 기말고사정리 07 - 통계적 가설 검정 (0) | 2022.06.05 |
