모 비율차 검정
A그룹에서의 비율과 B그룹에서의 비율이 같은지 검정
📜예제자료
x=c(100,170)
n=c(300,400)(x [1], n [1]) = 300번 중에 100번 성공했다 라는 뜻
(x [2], n [2]) = 400번 중에 170번 성공했다 라는 뜻.
📗모 비율차 검정
prop.test(x,n)
💡해석
- 추정 : D후보의 A도시에서의 지지율은 33%, B도시에서의 지지율은 42.5$% 이다.
- 가설 검정
- 가설
- H0 : A도시와 B도시에서의 지지율은 같다. [귀무가설]
- H1: A도시와 B도시에서의 지지율은 다르다. [대립 가설]
- 유의 수준 α= 0.05
- 검정 통계량 =5.6988
- P-value = 0.01698 < α => 귀무가설을 기각, 대립 가설을 채택
- 결론 : 유의 수준 5%에서 A도시에서의 지지율과 B도시에서의 지지율은 다르다고 할 수 있다. B도시에서의 지지율이 A도시에서의 지지율보다 높다고 할 수 있다.
- 가설
📗R프로그래밍을 이용
Z_prop = function(x,n){
p1=x[1]/n[1]
p2=x[2]/n[2]
p=(x[1]+x[2]) / (n[1]+n[2])
se=sqrt(p*(1-p)*(1/n[1]+1/n[2]))
Z=(p1-p2)/se
pvalue=2*(1-pnorm(abs(Z)))
cat(" =========== 비율차 검정 ==============","\n","\n")
cat(" 비율차 = ", p1-p2,"Z= ",Z,"P-value=",pvalue,"\n")
}
Z_prop(x,n)

R프로그래밍 실행결과 P값은 α보다 작다. 따라서 귀무가설을 기각,
📕연습문제 1
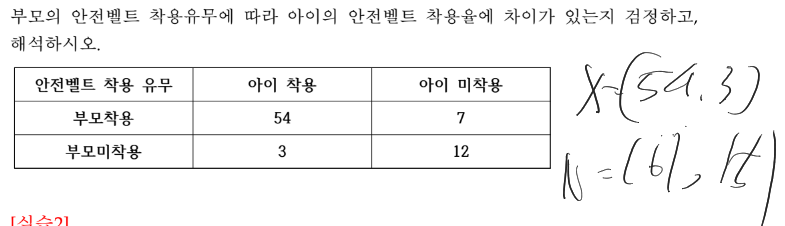
부모의 착용 유무에 따른 아이의 안전벨트 착용률이기 때문에
부모가 착용한 경우 아이가 착용할 확률은 54/61
부모가 착용하지 않은 경우 아이가 착용할 확률은 3/15
x=c(54,3) ##착용할 확률
n=c(61,15) ##전체 경우의 수📗모 비율차 검정
prop.test(x,n)
💡해설
- 추정 : 부모가 착용한 경우 아이의 착용 확률은 88%이고, 부모가 착용하지 않은 경우 아이의 착용 확률은 20%이다.
- 가설 검정
- 가설
- H0 : 부모가 착용 한경 우와 부모가 착용하지 않은 경우 아이의 착용 확률은 같다. [귀무가설]
- H1 : 부모가 착용 한경 우와 부모가 착용하지 않은 경우 아이의 착용 확률은 다르다. [대립 가설]
- 유의 수준 α =0.05
- 검정 통계량 = 26.607
- P-value < α => 귀무가설 기각, 대립 가설 채택
- 결론 : 유의 수준 5%에서 부모가 착용한 경우 아이의 착용 확률과 부모가 착용하지 않은 경우 아이의 착용 확률은 다르다고 할 수 있다. 부모가 착용한 경우 아이의 착용 확률이 높다고 할 수 있다.
- 가설
📕연습문제 2

도시지역에서의 지지자 확률은 2400/5000
농촌지역에서의 지지자 확률은 1200/2000
x=c(2400,1200)
n=c(5000,2000)📗모비율 평균 차 검정
prop.test(x,n)
💡해석
- 추정 : 도시에서의 지지 확률은 48%이고, 농촌에서의 지지확률은 60%이다.
- 가설검정
- 가설
- H0 : 도시에서의 지지 확률과 농촌에서의 지지 확률은 같다. [귀무가설]
- H1 : 도시에서의 지지 확률과 농촌에서의 지지 확률은 다르다. [대립 가설]
- 유의 수준 α =0.05
- 검정 통계량 = 81.873
- P-value < α => 귀무가설 기각, 대립 가설 채택
- 결론 : 유의 수준 5%에서 도시에서의 지지 확률과 농촌에서의 지지 확률은 다르다고 할 수 있다. 농촌에서의 지지확률이 도시에서의 지지확률보다 높다고 할 수있다.
- 가설
'학교 > R프로그래밍' 카테고리의 다른 글
| R프로그래밍 기말고사 정리 13 - 모평균의 신뢰구간 (0) | 2022.06.14 |
|---|---|
| R프로그래밍 기말고사 정리 10 - 이표본 검정(이변량데이터) (0) | 2022.06.13 |
| R프로그래밍 기말고사정리 09- 이표본 검정 (0) | 2022.06.13 |
| R프로그래밍 기말고사 정리 08 - 이표본비율 (0) | 2022.06.13 |
| R프로그래밍 기말고사정리 07 - 통계적 가설 검정 (0) | 2022.06.05 |
모 비율차 검정
A그룹에서의 비율과 B그룹에서의 비율이 같은지 검정
📜예제자료
x=c(100,170) n=c(300,400)
(x [1], n [1]) = 300번 중에 100번 성공했다 라는 뜻
(x [2], n [2]) = 400번 중에 170번 성공했다 라는 뜻.
📗모 비율차 검정
prop.test(x,n)
💡해석
- 추정 : D후보의 A도시에서의 지지율은 33%, B도시에서의 지지율은 42.5$% 이다.
- 가설 검정
- 가설
- H0 : A도시와 B도시에서의 지지율은 같다. [귀무가설]
- H1: A도시와 B도시에서의 지지율은 다르다. [대립 가설]
- 유의 수준 α= 0.05
- 검정 통계량 =5.6988
- P-value = 0.01698 < α => 귀무가설을 기각, 대립 가설을 채택
- 결론 : 유의 수준 5%에서 A도시에서의 지지율과 B도시에서의 지지율은 다르다고 할 수 있다. B도시에서의 지지율이 A도시에서의 지지율보다 높다고 할 수 있다.
- 가설
📗R프로그래밍을 이용
Z_prop = function(x,n){ p1=x[1]/n[1] p2=x[2]/n[2] p=(x[1]+x[2]) / (n[1]+n[2]) se=sqrt(p*(1-p)*(1/n[1]+1/n[2])) Z=(p1-p2)/se pvalue=2*(1-pnorm(abs(Z))) cat(" =========== 비율차 검정 ==============","\n","\n") cat(" 비율차 = ", p1-p2,"Z= ",Z,"P-value=",pvalue,"\n") } Z_prop(x,n)

R프로그래밍 실행결과 P값은 α보다 작다. 따라서 귀무가설을 기각,
📕연습문제 1

부모의 착용 유무에 따른 아이의 안전벨트 착용률이기 때문에
부모가 착용한 경우 아이가 착용할 확률은 54/61
부모가 착용하지 않은 경우 아이가 착용할 확률은 3/15
x=c(54,3) ##착용할 확률 n=c(61,15) ##전체 경우의 수
📗모 비율차 검정
prop.test(x,n)
💡해설
- 추정 : 부모가 착용한 경우 아이의 착용 확률은 88%이고, 부모가 착용하지 않은 경우 아이의 착용 확률은 20%이다.
- 가설 검정
- 가설
- H0 : 부모가 착용 한경 우와 부모가 착용하지 않은 경우 아이의 착용 확률은 같다. [귀무가설]
- H1 : 부모가 착용 한경 우와 부모가 착용하지 않은 경우 아이의 착용 확률은 다르다. [대립 가설]
- 유의 수준 α =0.05
- 검정 통계량 = 26.607
- P-value < α => 귀무가설 기각, 대립 가설 채택
- 결론 : 유의 수준 5%에서 부모가 착용한 경우 아이의 착용 확률과 부모가 착용하지 않은 경우 아이의 착용 확률은 다르다고 할 수 있다. 부모가 착용한 경우 아이의 착용 확률이 높다고 할 수 있다.
- 가설
📕연습문제 2

도시지역에서의 지지자 확률은 2400/5000
농촌지역에서의 지지자 확률은 1200/2000
x=c(2400,1200) n=c(5000,2000)
📗모비율 평균 차 검정
prop.test(x,n)
💡해석
- 추정 : 도시에서의 지지 확률은 48%이고, 농촌에서의 지지확률은 60%이다.
- 가설검정
- 가설
- H0 : 도시에서의 지지 확률과 농촌에서의 지지 확률은 같다. [귀무가설]
- H1 : 도시에서의 지지 확률과 농촌에서의 지지 확률은 다르다. [대립 가설]
- 유의 수준 α =0.05
- 검정 통계량 = 81.873
- P-value < α => 귀무가설 기각, 대립 가설 채택
- 결론 : 유의 수준 5%에서 도시에서의 지지 확률과 농촌에서의 지지 확률은 다르다고 할 수 있다. 농촌에서의 지지확률이 도시에서의 지지확률보다 높다고 할 수있다.
- 가설
'학교 > R프로그래밍' 카테고리의 다른 글
| R프로그래밍 기말고사 정리 13 - 모평균의 신뢰구간 (0) | 2022.06.14 |
|---|---|
| R프로그래밍 기말고사 정리 10 - 이표본 검정(이변량데이터) (0) | 2022.06.13 |
| R프로그래밍 기말고사정리 09- 이표본 검정 (0) | 2022.06.13 |
| R프로그래밍 기말고사 정리 08 - 이표본비율 (0) | 2022.06.13 |
| R프로그래밍 기말고사정리 07 - 통계적 가설 검정 (0) | 2022.06.05 |
