📕문제
매일 아침, 세준이는 학교에 가기 위해서 차를 타고 D킬로미터 길이의 고속도로를 지난다. 이 고속도로는 심각하게 커브가 많아서 정말 운전하기도 힘들다. 어느 날, 세준이는 이 고속도로에 지름길이 존재한다는 것을 알게 되었다. 모든 지름길은 일방통행이고, 고속도로를 역주행할 수는 없다.
세준이가 운전해야 하는 거리의 최솟값을 출력하시오.
📕입력
첫째 줄에 지름길의 개수 N과 고속도로의 길이 D가 주어진다. N은 12 이하인 양의 정수이고, D는 10,000보다 작거나 같은 자연수이다. 다음 N개의 줄에 지름길의 시작 위치, 도착 위치, 지름길의 길이가 주어진다. 모든 위치와 길이는 10,000보다 작거나 같은 음이 아닌 정수이다. 지름길의 시작 위치는 도착 위치보다 작다.
📕출력
세준이가 운전해야 하는 거리의 최솟값을 출력하시오.
🔎문제해석
문제를 풀고 여러 블로그를 보니 문제를 푸는 방식이 다양해 보였다.
나는 DP를 이용해서 풀었다.
이 문제는 (출발위치, 도착 위치, 도로 길이)가 입력값이다. 여기서 해당 입력이 지름길인지 아닌지 파악하는 것이 중요하다.
- 입력받은 도로길이 vs 도착위치-출발위치(실제 도로길이)를 비교
- 입력받은 도착위치가 내가 목표로 하는 도착지보다 멀리있는지를 비교.
위에 2가지 기준으로 적절한 지름길을 뽑아서 저장해야 한다.
이러한 지름길을 나는 초기에 map을 사용해서 풀었지만, 테케는 다 통과했다!! [실제로는 통과하지 못함]
역시 map에 있는 key값에 중복되다 보니 엉뚱한 값이 들어간 것 같다.
그래서 잘 사용하지 않는 pair를 사용해서 벡터 안에 인자를 pair를 줘서 풀었다.
⚡구현

s는 출발지, f는 도착지, v는 지름길의 길이를 의미함.
if문 안에 본문은 위에 지름길의 여부를 판단하는 2가지 조건을 코드로 구현한 것이다.
만약 적절한 지름길이라면 vector P에 넣는다.
그러면 p에는 도착지마다 출발지와 지름길의 길이를 저장할 것이다.
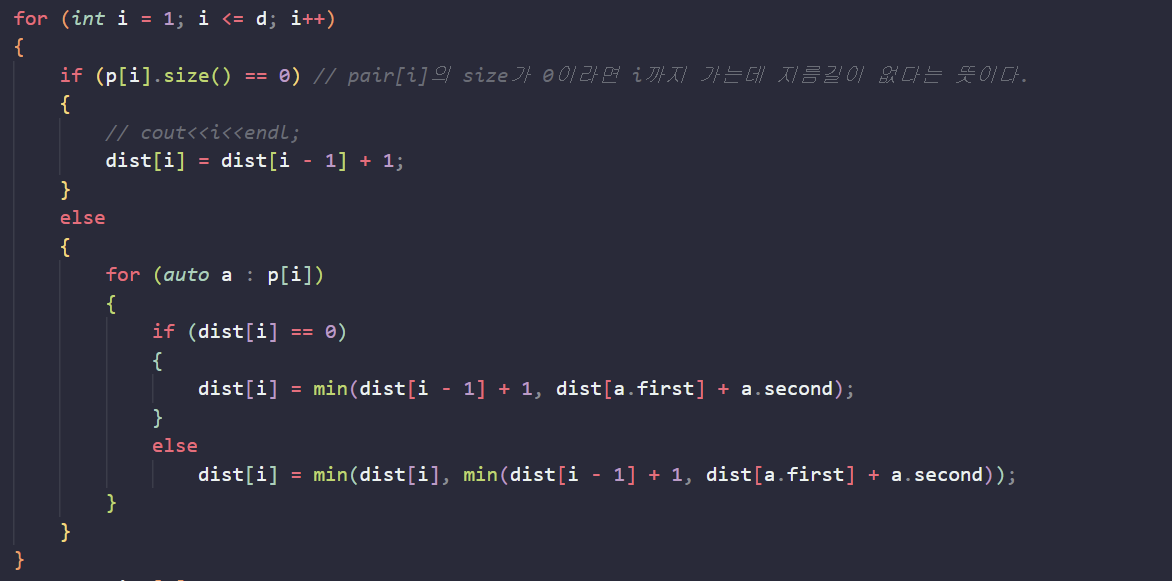
dist [i]는 i까지의 최소 거리를 저장하는 vector이다.
만약 dist [30]이면 1부터 30까지의 최소거리가 저장된다.
P [i]는 i를 도착지로 하는 지름길을 저장하는 벡터이다.
만약 그 사이즈가 0이라면 지름길이 없다는 뜻이므로 1km 전진한다.
사이즈가 0이 아니라면 P [i]에 있는 모든 순서쌍을 비교한다.
P [i]의 first는 출발지, second는 지름길의 길이다.
dist [i-1]+1은 지름길을 선택하지 않고 그냥 가는 경우.
지름길을 택하는 경우는 해당 지름길의 출발지점까지의 거리와 그 지름길의 길이인 a.second를 더한 값이다.
이 두 값을 비교해서 작은 값을 넣어주고, 이제 dist [i] 값이 0이 아니기 때문에 계속 비교해서 최솟값이 dist [i]에 들어가게 될 것이다.
📃코드
/*
백준 실버1 지름길
*/
#include <iostream>
#include <vector>
#include <algorithm>
#include <map>
using namespace std;
int n, d;
vector<int> dist;
int main()
{
cin >> n >> d;
dist.resize(d + 1, 0);
vector<pair<int, int>> p[d + 1]; // p[d+1]의 vector를 생성 p(d+1)은 vector의 size만 조절 pair의 사이즈는 조절하지못한것.
for (int i = 0; i < n; i++)
{
int s, f, v;
cin >> s >> f >> v;
if (f > d || f - s < v) //지름길이 부적절한 경우->
{ //만약 지름길의 도착점이 우리가 가고자 하는 지점보다 멀다면 굳이 필요가 없음.
// 지름길의 길이가 출발지점과 도착지점 사이의 실제거리보다 크다면 의미가 없음.
continue;
}
p[f].push_back(make_pair(s, v));
}
// DP사용 DP[i]는 i까지의 최소거리를 저장하고싶음.
// i까지의 지름길이 있는지 체크함.
for (int i = 1; i <= d; i++)
{
if (p[i].size() == 0) // pair[i]의 size가 0이라면 i까지 가는데 지름길이 없다는 뜻이다.
{
// cout<<i<<endl;
dist[i] = dist[i - 1] + 1;
}
else
{
for (auto a : p[i])
{
if (dist[i] == 0)
{
dist[i] = min(dist[i - 1] + 1, dist[a.first] + a.second);
}
else
dist[i] = min(dist[i], min(dist[i - 1] + 1, dist[a.first] + a.second));
}
}
}
cout << dist[d] << endl;
}✔느낀 점
- 다익스트라 알고리즘을 풀러 왔는데 Dp를 이용해서 풀어야 해서 깜짝 놀랐다.
- 이 문제는 다익스트라 알고리즘이 뭔지 몰라도 풀 수 있는 것 같다.
'CodingTest > Baekjoon' 카테고리의 다른 글
| [백준 17396] 백도어(C++) (0) | 2022.08.15 |
|---|---|
| [백준 1916] 최소비용 구하기(C++) (0) | 2022.08.13 |
| [백준 11404] 플루이드(C++) (0) | 2022.08.09 |
| [백준 2606] 바이러스(C++) (0) | 2022.08.06 |
| [백준 2468] 안전영역(C++) (0) | 2022.08.06 |
