📕문제
유섭이는 무척이나 게으르다. 오늘도 할 일을 모두 미뤄둔 채 열심히 롤을 하던 유섭이는 오늘까지 문제를 내야 한다는 사실을 깨달았다. 그러나 게임은 시작되었고 지는 걸 무척이나 싫어하는 유섭이는 어쩔 수 없이 백도어를 해 게임을 최대한 빠르게 끝내기로 결심하였다.
최대한 빨리 게임을 끝내고 문제를 출제해야 하기 때문에 유섭이는 최대한 빨리 넥서스가 있는 곳으로 달려가려고 한다. 유섭이의 챔피언은 총 N개의 분기점에 위치할 수 있다. 0번째 분기점은 현재 유섭이의 챔피언이 있는 곳을, N-1 번째 분기점은 상대편 넥서스를 의미하며 나머지 1, 2,...,N-2번째 분기점은 중간 거점들이다. 그러나 유섭이의 챔피언이 모든 분기점을 지나칠 수 있는 것은 아니다. 백도어의 핵심은 안 들키고 살금살금 가는 것이기 때문에 적 챔피언 혹은 적 와드(시야를 밝혀주는 토템), 미니언, 포탑 등 상대의 시야에 걸리는 곳은 지나칠 수 없다.
입력으로 각 분기점을 지나칠 수 있는지에 대한 여부와 각 분기점에서 다른 분기점으로 가는 데 걸리는 시간이 주어졌을 때, 유섭이가 현재 위치에서 넥서스까지 갈 수 있는 최소 시간을 구하여라.
📕입력
첫 번째 줄에 분기점의 수와 분기점들을 잇는 길의 수를 의미하는 두 자연수 N과 M이 공백으로 구분되어 주어진다.(1 ≤ N ≤ 100,000, 1 ≤ M ≤ 300,000)
두 번째 줄에 각 분기점이 적의 시야에 보이는지를 의미하는 N개의 정수 a0, a1, ..., aN-1가 공백으로 구분되어 주어진다. ai가 0이면 i 번째 분기점이 상대의 시야에 보이지 않는다는 뜻이며, 1이면 보인다는 뜻이다. 추가적으로 a0 = 0, aN-1 = 1이다., N-1번째 분기점은 상대 넥서스이기 때문에 어쩔 수 없이 상대의 시야에 보이게 되며, 또 유일하게 상대 시야에 보이면서 갈 수 있는 곳이다.
다음 M개의 줄에 걸쳐 세 정수 a, b, t가 공백으로 구분되어 주어진다. (0 ≤ a, b < N, a ≠ b, 1 ≤ t ≤ 100,000) 이는 a번째 분기점과 b번째 분기점 사이를 지나는데 t만큼의 시간이 걸리는 것을 의미한다. 연결은 양방향이며, 한 분기점에서 다른 분기점으로 가는 간선은 최대 1개 존재한다.
📕출력
첫 번째 줄에 유섭이의 챔피언이 상대 넥서스까지 안 들키고 가는데 걸리는 최소 시간을 출력한다. 만약 상대 넥서스까지 갈 수 없으면 -1을 출력한다.
🔎문제 해석
처음에는 아무 생각 없이 인접 행렬로 풀었는데 메모리 초과라는 결과가 나왔다.. 당황했었는데 사실 당연하게도
분기점과 분기점을 잇는 길의 수가 굉장히 많기 때문에 행렬로 구현한다면 엄청난 크기의 메모리를 잡아먹는다는 사실을 잊고 있었다. 그래서 허겁지겁 다른 방법인 인접 리스트로 풀었다. 인접 리스트라는 방식이 손에 잘 익지 않아서 굉장히 애를 먹었었고, 최댓값의 limit 값을 정하는 과정에서 굉장히 시행착오가 많았다,,ㅎㅎ(문제를 잘 읽어보자!)
🛑주의할 점
넥서스를 잇는 길은 양방향이며, 넥서스가 위치한 N-1번째 분기점에는 와드가 있는데, 그것을 0으로 초기화하는 것이 중요하다.
⚡구현
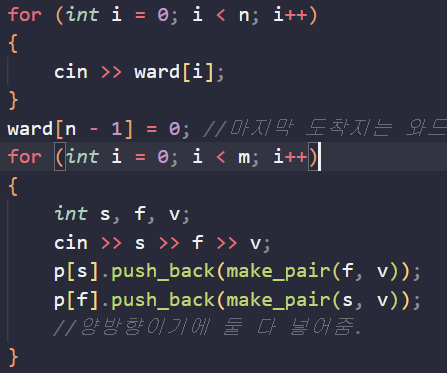
- 와드의 여부를 입력받고 넥서스의 위치에 있는 와드는 0으로 초기화해준다.
- 양방향으로 분기점을 입력받는다.

- PQ에는 오름차순으로 정렬되게끔 선언해줬다. pair의 first기준으로 오름차순으로 정렬했다.
- PQ의 top에 있는 원소를 뽑아주고, 거리 테이블과의 거리를 비교해서 더 현재 뽑은 원소의 거리가 길다면 탐색할 필요가 없다.
- for문을 통해서 현재 갈 수 있는 모든 지역을 탐색한다.
- 현재 가고자 하는 지역에 와드가 있다면 continue
- 와드에 걸리지 않았다면 다음 갈옷에 대한 거리와, 그 지역을 pair next에 넣어주고
- next의 거리가 거리 테이블보다 작다면 거리 테이블을 최신화해주고 PQ에 푸시해준다.

- 모든 과정이 끝났는데 만약 넥서스까지의 거리를 의미하는 d [n-1]이 INF라면 경로가 없다는 뜻이다.
- INF가 아니라면 그때의 값을 출력함.
📃코드
/*
백준 골드5 백도어
시간초과 나서 인접행렬 말고 인접리스트로 풀어야할듯.
우선순위큐를 이용해서 거리가 작은 순으로 queue에 넣기.
*/
#include <iostream>
#include <vector>
#include <algorithm>
#include <queue>
using namespace std;
#define INF 30000000001
int n, m;
vector<long long> ward;
vector<long long> d;
int answer = 0;
void back(int start);
int smallIdx(int start);
bool flag = 0;
int main()
{
cin >> n >> m;
vector<pair<int, long long>> p[n];
ward.resize(n, 0), d.resize(n, INF);
for (int i = 0; i < n; i++)
{
cin >> ward[i];
}
ward[n - 1] = 0; //마지막 도착지는 와드에 어쩔수 없이 보이기 때문에 0으로 바꿔줘야함.
for (int i = 0; i < m; i++)
{
int s, f, v;
cin >> s >> f >> v;
p[s].push_back(make_pair(f, v));
p[f].push_back(make_pair(s, v));
//양방향이기에 둘 다 넣어줌.
}
priority_queue<pair<long long, int>, vector<pair<long long, int>>, greater<pair<long long,int>>> PQ;
//PQ에는 (value,도착지)가 들어감.
PQ.push(make_pair(0, 0));
while (0 != PQ.size())
{
pair<long long, int> pa = PQ.top(); // p에다가 PQ에 top을 저장함. (value,도착지)
PQ.pop();
//나는 pq에 도착지와 거리를 넣고싶음.
if (pa.first > d[pa.second]) //도착지까지의 거리인 pa.first 와 거리테이블을 d[pa.second]를 비교함.
{
//만약 거리테이블보다 크다면 탐색할필요가 없음.
continue;
}
for (auto a : p[pa.second]) //현재 갈 수 있는 모든지역을 탐색함.
{ //p에는 (도착지,value)가 저장됨.
if (ward[a.first] == 1) //도착지가 와드시야에 보인다면 넘겨준다.
{
continue;
}
pair<long long, int> next = {a.second + pa.first, a.first}; //next에는 (도착지까지의 거리,도착지)가 저장됨.
if (next.first < d[a.first]) //현재 입력된 거리보다 거리테이블의 거리가 크다면 최신화해줌.
{
d[next.second] = next.first; //거리테이블을 최신화해줌.
PQ.push(next); //PQ에 넣어줌.
}
}
}
if (d[n - 1] == INF) //만약 넥서스까지의 거리가 INF면 도달 못한다는 뜻.
{
cout << -1;
}
else
cout << d[n - 1];
}✔느낀 점
- 인접 리스트로 짜는 방법도 연습해야 할 것 같다.
- 우선순위 큐와 pair를 묶어서 쓰니까 너무 어려웠다. <-- 이 부분도 이론에 대한 정리가 필요한 것 같다.
- 그리고 항상 문제에 경우의 수에 대한 최댓값을 계산해서 INF값을 넣어줘야겠다.
- 생각보다 어려웠다..!
'CodingTest > Baekjoon' 카테고리의 다른 글
| [백준 19583] - 싸이버개강총회 (0) | 2022.08.19 |
|---|---|
| [백준 1753] 최단경로(C++) (0) | 2022.08.16 |
| [백준 1916] 최소비용 구하기(C++) (0) | 2022.08.13 |
| [백준 1446] - 지름길(C++) (0) | 2022.08.12 |
| [백준 11404] 플루이드(C++) (0) | 2022.08.09 |
📕문제
유섭이는 무척이나 게으르다. 오늘도 할 일을 모두 미뤄둔 채 열심히 롤을 하던 유섭이는 오늘까지 문제를 내야 한다는 사실을 깨달았다. 그러나 게임은 시작되었고 지는 걸 무척이나 싫어하는 유섭이는 어쩔 수 없이 백도어를 해 게임을 최대한 빠르게 끝내기로 결심하였다.
최대한 빨리 게임을 끝내고 문제를 출제해야 하기 때문에 유섭이는 최대한 빨리 넥서스가 있는 곳으로 달려가려고 한다. 유섭이의 챔피언은 총 N개의 분기점에 위치할 수 있다. 0번째 분기점은 현재 유섭이의 챔피언이 있는 곳을, N-1 번째 분기점은 상대편 넥서스를 의미하며 나머지 1, 2,...,N-2번째 분기점은 중간 거점들이다. 그러나 유섭이의 챔피언이 모든 분기점을 지나칠 수 있는 것은 아니다. 백도어의 핵심은 안 들키고 살금살금 가는 것이기 때문에 적 챔피언 혹은 적 와드(시야를 밝혀주는 토템), 미니언, 포탑 등 상대의 시야에 걸리는 곳은 지나칠 수 없다.
입력으로 각 분기점을 지나칠 수 있는지에 대한 여부와 각 분기점에서 다른 분기점으로 가는 데 걸리는 시간이 주어졌을 때, 유섭이가 현재 위치에서 넥서스까지 갈 수 있는 최소 시간을 구하여라.
📕입력
첫 번째 줄에 분기점의 수와 분기점들을 잇는 길의 수를 의미하는 두 자연수 N과 M이 공백으로 구분되어 주어진다.(1 ≤ N ≤ 100,000, 1 ≤ M ≤ 300,000)
두 번째 줄에 각 분기점이 적의 시야에 보이는지를 의미하는 N개의 정수 a0, a1, ..., aN-1가 공백으로 구분되어 주어진다. ai가 0이면 i 번째 분기점이 상대의 시야에 보이지 않는다는 뜻이며, 1이면 보인다는 뜻이다. 추가적으로 a0 = 0, aN-1 = 1이다., N-1번째 분기점은 상대 넥서스이기 때문에 어쩔 수 없이 상대의 시야에 보이게 되며, 또 유일하게 상대 시야에 보이면서 갈 수 있는 곳이다.
다음 M개의 줄에 걸쳐 세 정수 a, b, t가 공백으로 구분되어 주어진다. (0 ≤ a, b < N, a ≠ b, 1 ≤ t ≤ 100,000) 이는 a번째 분기점과 b번째 분기점 사이를 지나는데 t만큼의 시간이 걸리는 것을 의미한다. 연결은 양방향이며, 한 분기점에서 다른 분기점으로 가는 간선은 최대 1개 존재한다.
📕출력
첫 번째 줄에 유섭이의 챔피언이 상대 넥서스까지 안 들키고 가는데 걸리는 최소 시간을 출력한다. 만약 상대 넥서스까지 갈 수 없으면 -1을 출력한다.
🔎문제 해석
처음에는 아무 생각 없이 인접 행렬로 풀었는데 메모리 초과라는 결과가 나왔다.. 당황했었는데 사실 당연하게도
분기점과 분기점을 잇는 길의 수가 굉장히 많기 때문에 행렬로 구현한다면 엄청난 크기의 메모리를 잡아먹는다는 사실을 잊고 있었다. 그래서 허겁지겁 다른 방법인 인접 리스트로 풀었다. 인접 리스트라는 방식이 손에 잘 익지 않아서 굉장히 애를 먹었었고, 최댓값의 limit 값을 정하는 과정에서 굉장히 시행착오가 많았다,,ㅎㅎ(문제를 잘 읽어보자!)
🛑주의할 점
넥서스를 잇는 길은 양방향이며, 넥서스가 위치한 N-1번째 분기점에는 와드가 있는데, 그것을 0으로 초기화하는 것이 중요하다.
⚡구현

- 와드의 여부를 입력받고 넥서스의 위치에 있는 와드는 0으로 초기화해준다.
- 양방향으로 분기점을 입력받는다.

- PQ에는 오름차순으로 정렬되게끔 선언해줬다. pair의 first기준으로 오름차순으로 정렬했다.
- PQ의 top에 있는 원소를 뽑아주고, 거리 테이블과의 거리를 비교해서 더 현재 뽑은 원소의 거리가 길다면 탐색할 필요가 없다.
- for문을 통해서 현재 갈 수 있는 모든 지역을 탐색한다.
- 현재 가고자 하는 지역에 와드가 있다면 continue
- 와드에 걸리지 않았다면 다음 갈옷에 대한 거리와, 그 지역을 pair next에 넣어주고
- next의 거리가 거리 테이블보다 작다면 거리 테이블을 최신화해주고 PQ에 푸시해준다.

- 모든 과정이 끝났는데 만약 넥서스까지의 거리를 의미하는 d [n-1]이 INF라면 경로가 없다는 뜻이다.
- INF가 아니라면 그때의 값을 출력함.
📃코드
/* 백준 골드5 백도어 시간초과 나서 인접행렬 말고 인접리스트로 풀어야할듯. 우선순위큐를 이용해서 거리가 작은 순으로 queue에 넣기. */ #include <iostream> #include <vector> #include <algorithm> #include <queue> using namespace std; #define INF 30000000001 int n, m; vector<long long> ward; vector<long long> d; int answer = 0; void back(int start); int smallIdx(int start); bool flag = 0; int main() { cin >> n >> m; vector<pair<int, long long>> p[n]; ward.resize(n, 0), d.resize(n, INF); for (int i = 0; i < n; i++) { cin >> ward[i]; } ward[n - 1] = 0; //마지막 도착지는 와드에 어쩔수 없이 보이기 때문에 0으로 바꿔줘야함. for (int i = 0; i < m; i++) { int s, f, v; cin >> s >> f >> v; p[s].push_back(make_pair(f, v)); p[f].push_back(make_pair(s, v)); //양방향이기에 둘 다 넣어줌. } priority_queue<pair<long long, int>, vector<pair<long long, int>>, greater<pair<long long,int>>> PQ; //PQ에는 (value,도착지)가 들어감. PQ.push(make_pair(0, 0)); while (0 != PQ.size()) { pair<long long, int> pa = PQ.top(); // p에다가 PQ에 top을 저장함. (value,도착지) PQ.pop(); //나는 pq에 도착지와 거리를 넣고싶음. if (pa.first > d[pa.second]) //도착지까지의 거리인 pa.first 와 거리테이블을 d[pa.second]를 비교함. { //만약 거리테이블보다 크다면 탐색할필요가 없음. continue; } for (auto a : p[pa.second]) //현재 갈 수 있는 모든지역을 탐색함. { //p에는 (도착지,value)가 저장됨. if (ward[a.first] == 1) //도착지가 와드시야에 보인다면 넘겨준다. { continue; } pair<long long, int> next = {a.second + pa.first, a.first}; //next에는 (도착지까지의 거리,도착지)가 저장됨. if (next.first < d[a.first]) //현재 입력된 거리보다 거리테이블의 거리가 크다면 최신화해줌. { d[next.second] = next.first; //거리테이블을 최신화해줌. PQ.push(next); //PQ에 넣어줌. } } } if (d[n - 1] == INF) //만약 넥서스까지의 거리가 INF면 도달 못한다는 뜻. { cout << -1; } else cout << d[n - 1]; }
✔느낀 점
- 인접 리스트로 짜는 방법도 연습해야 할 것 같다.
- 우선순위 큐와 pair를 묶어서 쓰니까 너무 어려웠다. <-- 이 부분도 이론에 대한 정리가 필요한 것 같다.
- 그리고 항상 문제에 경우의 수에 대한 최댓값을 계산해서 INF값을 넣어줘야겠다.
- 생각보다 어려웠다..!
'CodingTest > Baekjoon' 카테고리의 다른 글
| [백준 19583] - 싸이버개강총회 (0) | 2022.08.19 |
|---|---|
| [백준 1753] 최단경로(C++) (0) | 2022.08.16 |
| [백준 1916] 최소비용 구하기(C++) (0) | 2022.08.13 |
| [백준 1446] - 지름길(C++) (0) | 2022.08.12 |
| [백준 11404] 플루이드(C++) (0) | 2022.08.09 |
