문제
교재의 내용과 강의자료를 참고하여 0-1 배낭 문제를 해결하는 알고리즘의 구현을 완성하시오.
강의자료에서 knapsack2() 또는 knapsack3()를 참조할 것.
단, 입력값은 단위 무게당 이익의 순서로 정렬되어 있지 않음에 유의하시오.
또한, 알고리즘 실행 결과의 출력은 알고리즘의 실행 과정에서 결과 테이블 P에 저장한
무게(i) 또는 이익(j)이 0이 아닌 모든 항목 P[i][j]를 (i, j)의 오름차순으로 모두 출력한다는 것에 주의하시오.
입력
첫 번째 줄에 아이템의 개수 n이 주어진다.
두 번째 줄에 n개의 무게 w[i]가 주어진다.
세 번째 줄에 n개의 이익 p[i]가 주어진다.
네 번째 줄에 배낭 무게의 개수 T가 주어진다.
이후로 T개의 줄에 한 줄에 하나씩 배낭 무게 W가 주어진다.
출력
주어진 배낭 무게 W 각각에 대해 다음과 같이 출력한다.
첫 줄에 최대 이익 maxprofit을 출력한다.
이후로 알고리즘의 실행과정에서 결과 테이블 P에 저장한
무게(i) 또는 이익(j)이 0이 아닌 모든 항목 P [i][j]를 (i, j)의 오름차순으로 모두 출력한다
문제 해석
0-1 배낭 문제는 보석의 무게를 쪼갤 수 없다. 그래서 단위 무게당 이익을 기준으로 탐욕적으로 접근한다면 언제나 최적 값을 도출할 수는 없다. 따라서 0-1 배낭 문제를 해결하기 위해서는 탐욕 법이 아닌 동적 계획법으로 접근해야 한다.
예를 들어서 설명해보겠다.
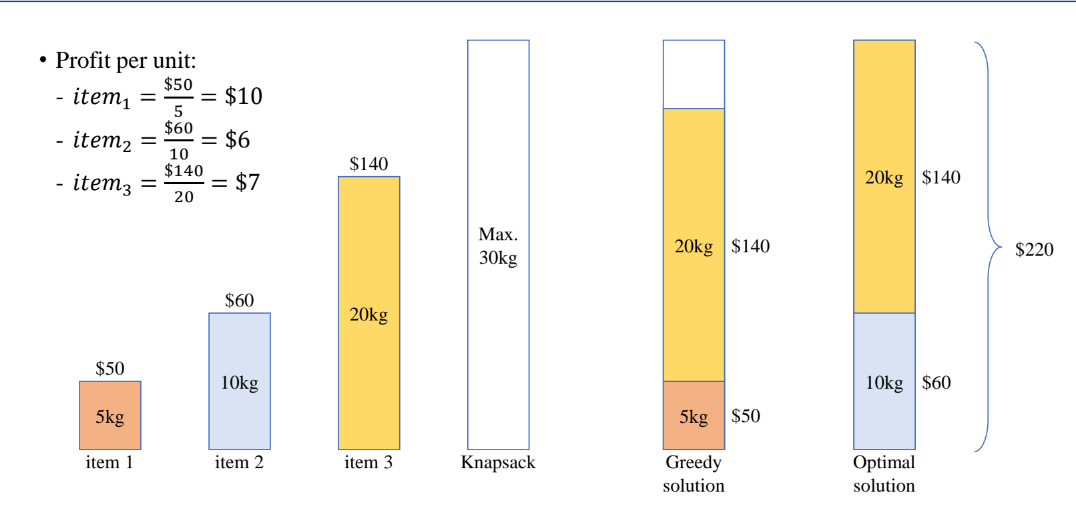
Fractional Knapsack문제라면 무게당 이익이 큰 순서대로 넣어서 하는 탐욕적인 접근 방법이 최적의 설루션일 것이다. 하지만 0-1 knapsack문제일 때는 보석을 쪼갤 수가 없기 때문에 무게당 이익이 큰 순서대로 넣는다면 가방의 용량을 낭비하는 현상이 생길 수도 있다. 따라서 탐욕 법으로 접근하면 안 된다.
구현
- 단위 무게당 이익이 큰 순서대로 정렬함.
- 보석을 담은 경우와 안 담을 경우를 구분함
- 만약 보석을 담은 경우
- 탐색해야 할 보석의 수를 한 개 줄여줌. (n->n-1)
- 보석을 담았으니 가방의 용량에서 담은 보석의 무게를 빼줌.(W-w [i])
- 만약 보석을 담지 않은 경우
- 담지 않아도 탐색해야 할 보석의 수는 한 개 줄어듬.(n->n-1)
- 보석을 담지 않았으니 가방의 용량에서 보석의 무게를 빼줄 필요가 없음.(W->W)
- 만약 보석을 담은 경우
- 종료 조건은 다음과 같다.
- n이 0일 때! 즉 모든 보석을 탐색했을 때이다.
- W <=0일 때! 즉 가방의 용량을 넘길 때이다.
코드
/*
1.배낭을 단위 무게별로 정렬시킴.
2.함수 내에서n은 남은 보석의 개수 w는 내가 담을수있는 무게.
3.DP를 사용하는데 담는경우와 안담는경우를 구분함
4.담았을때는 (n->n-1) 그리고 (w->w-w[i])로 바꿔줌 담았으니까
5.담지않았을떄는 (n->n-1), (w->w-w[i])로 바꿔줌.
6 P[i][w]의 값은 P[i-1][w] (담지 않은경우) Vs P[i-1][w-w[i]] + P[i]를 비교해야한다. 조건은 w[i]가 w보다 작거나 같아야 한다.
7. n==0 혹은 W=0이 되었을때 중단하면 된다. n=0이라는 뜻은 이제 더이상 보석을 담을 수가 없다는 뜻이고 w=0이면 가방이 꽉 찼다는 뜻이다.
*/
#include <iostream>
#include <vector>
#include <algorithm>
#include <map>
using namespace std;
int n, W,lvalue,rvalue;
vector<int>profit;
vector<int>weight;
int Knapsack3(int n, int W, vector<int>& w, vector<int>& p, map<pair<int, int>, int>& P);
int main()
{
cin >> n;
profit.resize(n + 1);
weight.resize(n + 1);
map<pair<int, int>, int>P;
for (int i = 1; i <= n; i++)
{
cin >> weight[i];
}
for (int i = 1; i <= n; i++)
{
cin >> profit[i];
}
for (int i = 1; i <= n; i++)
{
for (int j = i + 1; j <= n; j++)
{
if (profit[i] / weight[i] < profit[j] / weight[j])
{
swap(profit[i], profit[j]);
swap(weight[i], weight[j]);
}
}
}
int t;
cin >> t;
for (int i = 0; i < t; i++)
{
cin >> W;
int cnt = 0;
cout << Knapsack3(n, W, weight, profit, P) << endl;
//lvalue = 0, rvalue = 0;
//cout << P.size();
for (auto iter = P.begin(); iter != P.end(); iter++)
{
cout << iter->first.first << " " << iter->first.second << " " << iter->second;
cnt++;
if (i == t - 1 && cnt == P.size())
{
continue;
}
else cout << endl;
}
P.erase(P.begin(), P.end());
}
}
int Knapsack3(int n, int W, vector<int>& w, vector<int>& p, map<pair<int, int>, int>& P) //map은 n으로 오름차순 정렬함.
{
if (n == 0 || W <= 0)
{
return 0;
}
//lvalue = 담지 않앗을댸 rvalue는 담았을때
int lvalue = (P.find(make_pair(n - 1, W)) != P.end()) ? //map에 값이 있다면 그대로 lvalue에 넣어주면됨. 없다면 함수로 구함.
P[make_pair(n - 1, W)] : Knapsack3(n - 1, W, w, p, P);
int rvalue = (P.find(make_pair(n - 1, W-w[n])) != P.end()) ? //map에 값이 있다면 그대로 rvalue에 넣어주고, 없다면 함수로 구함.
P[make_pair(n - 1, W-w[n])] : Knapsack3(n - 1, W - w[n], w, p, P);
if (w[n] > W) //w[n]>w 내가 담을려는 무게인 w[n]이 잔여무게W보다 무겁다면 자동으로 담지 않는 쪽을 택해야함.
P[make_pair(n, W)] = lvalue;
else
P[make_pair(n, W)] = max(lvalue, rvalue + p[n]); //그렇지 않다면 담을때와 안담을때를 비교해줌.
return P[make_pair(n, W)];
}👀요약
- lvalue는 내가 담지 않았을때의 값이며 만약 그때의 값이 저장되어있다면 바로 꺼내서 쓰고, 없다면 함수를 통해서 구한다.
- rvalue는 내가 담았을때의 값이며 만약 그때의 값이 저장되어있다면 바로 꺼내서 쓰고, 없다면 함수를 통해서 구한다.
- w[n]은 현재 내가 담을려는 가방의 무게이다.
- 만약 w[n]이 잔여공간 W보다 무겁다면 담을수없으므로 바로 lvalue를 넣어준다.
- 만약 w[n]이 잔여공간 W보다 가볍다면 담을수있다.
- 그래서 이전에 담지않았을떄의 값과 담았을때의 값을 비교해서 큰 값을 넣어준다.
'Skils > Algorithm' 카테고리의 다른 글
| [C++]알고리즘 - 기사의 여행 문제와 해밀턴 경로 (0) | 2022.05.28 |
|---|---|
| 알고리즘[C++] 0-1 knapsack problem with Backtracking(백트래킹) (0) | 2022.05.23 |
| 알고리즘[C++]-Hamiltonian Problem(해밀턴 회로 문제) (2) | 2022.05.16 |
| 알고리즘(C++)-Backtracking을 이용한 영역칠하기(m-coloring) (0) | 2022.05.16 |
| 알고리즘[C++]- Backtracking을 이용한 부분집합의 합(subset_sum)순서쌍 구하기. (0) | 2022.05.15 |
