문제
주어진 무방향 무가 중치 그래프 G = (V, E)에서
해밀턴 회로의 개수를 출력하시오.
Algorithm 5.6을 구현할 때, 출발 정점은 1로 간주한다는 것을 주의하시오.
입력
첫째 줄에 정점의 개수 n과 간선의 개수 m이 주어진다.
둘째 줄부터 m개의 간선이 주어진다.
출력
첫째 줄에 해밀턴 회로의 개수를 출력한다.
문제 해석
이 문제를 풀기 위해서는 해밀턴 회로와 해밀턴 경로의 차이를 알아야 한다.
해밀턴 회로 VS 해밀턴 경로
해밀턴 회로
한 정점에서 출발을 해 모든 정점을 딱 한 번씩 방문하고 다시 출발 정점으로 돌아와야 한다.
출발 정점과 해밀턴 회로는 무관하다.
해밀턴 경로
해밀턴 경로는 해밀턴 회로와 다르게 출발 정점에 따라 값이 다르다.
한 정점에서 출발해서 모든 정점을 한 번씩 방문하면 그때의 방문 순서가 해밀턴 경로이다.
해밀턴 회로와 다르게 마지막 정점에서 다시 출발 정점으로 갈 필요는 없다.
아래 그림은 어느 정점에서 출발하든 마지막 정점을 방문하고 다시 출발정점으로 돌아가는 경우가 있기 때문에 해밀턴 회로라고 할 수 있다.
ex) 1->2->3->6->5->4는 해밀턴 회로이자 해밀턴 경로라고 할 수 있다.
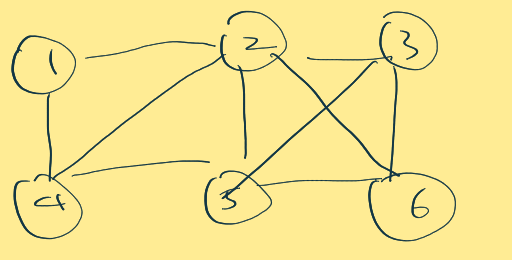
아래 그림은
해밀턴 회로에는 해당되지 않는다.
하지만 ex) 1->5->2->3->4는 해밀턴 경로라고 할 수 있다.
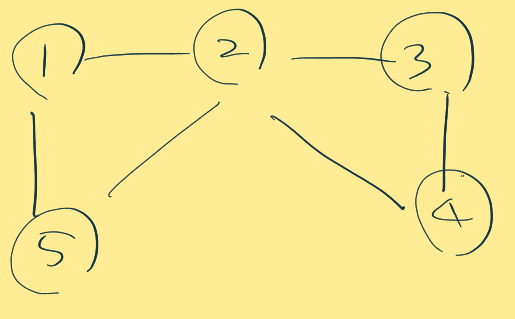
이제 해밀턴 회로와 해밀턴 경로의 차이를 인지했을 것입니다.
설계
- Backtracking을 이용해서 모든 노드를 방문하자!
- 적절한 가지치기를 통해서 불필요한 탐색을 줄이자!
- 가지치기 조건
- 지금 방문한 노드가 이전에 방문한 노드였다면 탐색할 필요가 없다.
- 만약 모든 노드를 방문했다면 마지막 노드에서 출발 정점까지의 경로의 여부를 따지자.
- 만약 경로가 있다면? 해밀턴 회로의 수와 해밀턴 경로의 수를 증가시킨다.
- 만약 경로가 없다면? 해밀턴 경로의 수만 증가시킨다.
- 가지치기 조건
- 종료 조건은 모든 노드를 방문한 경우, 즉 간선의 수가 정점의 개수 -1일 때이다.
코드
#include <iostream>
#include <vector>
using namespace std;
int G, V,cnt=0;
vector < vector<int>>graph;
vector<int>visit;
bool promising(int i);
void hamiltonian(int i);
int main()
{
cin >> G >> V;
graph.resize(G + 1, vector<int>(G + 1, 0));
visit.resize(G + 1);
for (int i = 0; i < V; i++)
{
int s, f;
cin >> s >> f;
graph[s][f] = 1, graph[f][s] = 1;
}
visit[0] = 1; //visit[0]의 값은 출발정점을 의미함. 문제에서 출발정점은 1로 명시하였기 때문에 1로 초기화함.
hamiltonian(0);
cout << cnt;
}
bool promising(int i) //조건이 2개있음. 일단 마지막 도착지일때는 그 도착지와 1이 연결되어있어야함.
{
//i가 1일 때
bool flag;
//flag = 1;
int idx=1;
if (i == G - 1 && graph[visit[G-1]][visit[0]]!=1) //i가현재정점
{
flag = false;
}
else if (i>0&&graph[visit[i]][visit[i-1]]!= 1)
{
flag = false;
}
else //여기서는 돌아줘야함. 마지막노드가 아니니까
{
flag = true;
while (idx < i) //내가 방문한 노드가 i임.
{
if (visit[idx] == visit[i]) //조건은 두개가 연결되어있어야하고 방문한곳이아니여야함.
{
flag = false;
}
idx++;
}
}
return flag;
}
void hamiltonian(int i)
{
if (promising(i)) //조건 검사를 햇을 떄 적절한가?
{
if (i == G - 1) // 간선의 개수가 n-1개 일때 종료해야함
{
cnt++; //경로 추가
}
else
{
for (int j = 2; j <= G; j++)
{
visit[i + 1] = j; //현재 방문한곳에 정점을 찍어줌. 정점이 겹치면 재귀 탈출하고 다시 반복문 돌아감.
hamiltonian(i + 1);
}
}
}
}해밀턴 회로와 해밀턴 경로의 차이만 안다면 쉽게 풀 수 있는 문제이다.
'Skils > Algorithm' 카테고리의 다른 글
| 알고리즘[C++] 0-1 knapsack problem with Backtracking(백트래킹) (0) | 2022.05.23 |
|---|---|
| 알고리즘[C++] 0-1 knapsack with 동적계획법(Dynamic programming) (0) | 2022.05.22 |
| 알고리즘(C++)-Backtracking을 이용한 영역칠하기(m-coloring) (0) | 2022.05.16 |
| 알고리즘[C++]- Backtracking을 이용한 부분집합의 합(subset_sum)순서쌍 구하기. (0) | 2022.05.15 |
| [C++]-백트래킹(Backtracking)이란? + n-Queens문제 (0) | 2022.05.06 |
