문제
주어진 평면 그래프 G = (V, E)에 대해서
인접한 지역을 서로 다른 색으로 색칠하기 위해 필요한 최소 색의 수 m의 값과
해당하는 m의 값으로 색칠할 수 있는 경우의 수를 출력하시오.
단, 그래프의 입력은 간선의 집합으로 주어지고, 주어진 그래프는 평면 그래프라고 가정해도 된다.
입력
첫 줄에 정점의 수 n과 간선의 수 k가 주어진다.
둘째 줄부터 k개의 간선이 주어진다.
출력
첫째 줄에 색칠 가능한 최소의 m값을 출력한다.
둘째 줄에 해당 m값으로 색칠할 수 있는 경우의 수를 출력한다.
문제 해석
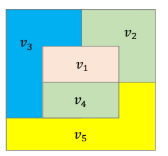
- 그림과 같이 인접해 있는 영역끼리는 서로 다른 색을 칠해야 한다.
- 여기서 인접한다의 의미는 영역들끼리 가로 세로중 하나라도 맞닿아있어야 한다.
- v1과 v3, v2는 가로 세로 중 한 영역이 맞닿아있지만, v2와 v4는 가로, 세로 중 한 영역도 맞닿아있지 않기 때문에 서로 같은 색깔을 칠 할 수 있는 것이다.
설계
- 각 영역들이 인접한 지 안 한 지를 따져준다. 인접 행렬의 개념을 사용한다. 2차원 배열을 만들어서 예를 들어 vi과 vj가 인접하다면 graph [i][j]=1 && graph [j][i]=1로 초기화하고 인접하지 않다면 graph [i][j]=0으로 초기 화하면 된다.
- Backtracking을 이용해서 모든 경우의 수를 따져준다.
- pruning을 이용해서 불필요한 탐색을 없앤다.
- 가지치기 조건
- 두 영역이 인접해있고, 컬러가 같을 경우는 조건에 부합하지 않으므로 가지치기를 통해서 경우의 수를 제거한다.
- 종료 조건
- 칠한 영역의 수가 정점의 개수와 같아질 때 종료하면 된다.
- 가지치기 조건
내가 헷갈린 부분
문제 조건에서 영역을 칠 할 수 있는 최소한의 색깔을 구하고, 최소한의 색깔로 칠 할 수 있는 경우의 수를 구해야 한다.
여기서 나는 최소한의 색깔을 구하는 방법을 처음으로 영역을 다 칠하게 된 경우의 색깔의 수라고 생각했다.
하지만 이렇게 구하니까 계속 wrong answer가 떴다...ㅎㅎ
그래서 다시 생각한 방법이 색깔을 하나씩 추가해서 만약 색깔이 하나일 때 해당 영역을 칠하지 못한다면 색깔을 하나씩 추가해줬다. 이렇게 하니까 정답이 나왔다ㅎㅎ,,
처음으로 완료한 경우가 bestcase가 아닐 수도 있다는 것을 깨달았다.
코드
#include <iostream>
#include <vector>
using namespace std;
int N, k, cnt = 0,val=0,opt=0;
vector<vector<int>>g;
vector<int>color;
bool promising(int i);
void draw(int col, int m, int &opt);
int main()
{
cin >> N >> k;
g.resize(N+1, vector<int>(N+1, 0));
for (int i = 0; i < k; i++)
{
int s, f = 0;
cin >> s >> f;
g[s][f] = 1, g[f][s] = 1;
}
color.resize(N+1, 0);
int idx = 0;
while (1) //계속 반복해서 색깔을 추가해줌.
{
draw(idx, val, opt);
if(opt==1) //val값으로 다 칠한 경우 그때의 val값이 최소의 색깔이고 cnt가 최소의 색깔로 칠할 수 있는 경우의수
{
cout << val<<endl;
cout << cnt;
break;
}
else
val++;
}
//cout <<m<<endl<<cnt;
}
bool promising(int i)
{
int j = 1;
bool flag = true;
while (i > j&&flag)
{
if (g[i][j] == 1 && color[i] == color[j]) //가지치기 조건. 인접했고, 색깔이 같을 경우
{
//return 0; 바로 종료하면 안됨 끝까지 탐색을 못함. 한번이라도 if문을 들어가면 칠하면안되는거니까 flag에 0을 넣어줌.
flag = false;
}
j++;
}
return flag;
}
void draw(int i,int m , int &opt)
{
if (promising(i))//적절하면 실행하고 적절하지 않으면 넘어감.
{
if (i == N) //끝까지 다 칠했을 때
{
cnt++;
opt = 1;
}
else
{
for (int j = 1; j <=m; j++) //지정해준 m까지 반복문을 돌림
{
color[i+1] = j; //i+1 에 j를 칠하고 draw(i+1)호출했는데 적절하지 않으면 다시 되돌아와서 다음색깔을 칠해줌.
draw(i+1,m,opt); //다음칸에 칠하고 적절한지 검사함.
}
}
}
}점점 Backtracking을 연습하니 점점 익숙해지는 느낌이 든다. 가지치기 조건과 재귀만 잘 생각하면 쉽게 풀 수 있는 문제였다.
'Skils > Algorithm' 카테고리의 다른 글
| 알고리즘[C++] 0-1 knapsack with 동적계획법(Dynamic programming) (0) | 2022.05.22 |
|---|---|
| 알고리즘[C++]-Hamiltonian Problem(해밀턴 회로 문제) (2) | 2022.05.16 |
| 알고리즘[C++]- Backtracking을 이용한 부분집합의 합(subset_sum)순서쌍 구하기. (0) | 2022.05.15 |
| [C++]-백트래킹(Backtracking)이란? + n-Queens문제 (0) | 2022.05.06 |
| 알고리즘[C++] - 허프만 코드(Huffman Code ) (0) | 2022.05.01 |
문제
주어진 평면 그래프 G = (V, E)에 대해서
인접한 지역을 서로 다른 색으로 색칠하기 위해 필요한 최소 색의 수 m의 값과
해당하는 m의 값으로 색칠할 수 있는 경우의 수를 출력하시오.
단, 그래프의 입력은 간선의 집합으로 주어지고, 주어진 그래프는 평면 그래프라고 가정해도 된다.
입력
첫 줄에 정점의 수 n과 간선의 수 k가 주어진다.
둘째 줄부터 k개의 간선이 주어진다.
출력
첫째 줄에 색칠 가능한 최소의 m값을 출력한다.
둘째 줄에 해당 m값으로 색칠할 수 있는 경우의 수를 출력한다.

문제 해석
- 그림과 같이 인접해 있는 영역끼리는 서로 다른 색을 칠해야 한다.
- 여기서 인접한다의 의미는 영역들끼리 가로 세로중 하나라도 맞닿아있어야 한다.
- v1과 v3, v2는 가로 세로 중 한 영역이 맞닿아있지만, v2와 v4는 가로, 세로 중 한 영역도 맞닿아있지 않기 때문에 서로 같은 색깔을 칠 할 수 있는 것이다.
설계
- 각 영역들이 인접한 지 안 한 지를 따져준다. 인접 행렬의 개념을 사용한다. 2차원 배열을 만들어서 예를 들어 vi과 vj가 인접하다면 graph [i][j]=1 && graph [j][i]=1로 초기화하고 인접하지 않다면 graph [i][j]=0으로 초기 화하면 된다.
- Backtracking을 이용해서 모든 경우의 수를 따져준다.
- pruning을 이용해서 불필요한 탐색을 없앤다.
- 가지치기 조건
- 두 영역이 인접해있고, 컬러가 같을 경우는 조건에 부합하지 않으므로 가지치기를 통해서 경우의 수를 제거한다.
- 종료 조건
- 칠한 영역의 수가 정점의 개수와 같아질 때 종료하면 된다.
- 가지치기 조건
내가 헷갈린 부분
문제 조건에서 영역을 칠 할 수 있는 최소한의 색깔을 구하고, 최소한의 색깔로 칠 할 수 있는 경우의 수를 구해야 한다.
여기서 나는 최소한의 색깔을 구하는 방법을 처음으로 영역을 다 칠하게 된 경우의 색깔의 수라고 생각했다.
하지만 이렇게 구하니까 계속 wrong answer가 떴다...ㅎㅎ
그래서 다시 생각한 방법이 색깔을 하나씩 추가해서 만약 색깔이 하나일 때 해당 영역을 칠하지 못한다면 색깔을 하나씩 추가해줬다. 이렇게 하니까 정답이 나왔다ㅎㅎ,,
처음으로 완료한 경우가 bestcase가 아닐 수도 있다는 것을 깨달았다.
코드
#include <iostream> #include <vector> using namespace std; int N, k, cnt = 0,val=0,opt=0; vector<vector<int>>g; vector<int>color; bool promising(int i); void draw(int col, int m, int &opt); int main() { cin >> N >> k; g.resize(N+1, vector<int>(N+1, 0)); for (int i = 0; i < k; i++) { int s, f = 0; cin >> s >> f; g[s][f] = 1, g[f][s] = 1; } color.resize(N+1, 0); int idx = 0; while (1) //계속 반복해서 색깔을 추가해줌. { draw(idx, val, opt); if(opt==1) //val값으로 다 칠한 경우 그때의 val값이 최소의 색깔이고 cnt가 최소의 색깔로 칠할 수 있는 경우의수 { cout << val<<endl; cout << cnt; break; } else val++; } //cout <<m<<endl<<cnt; } bool promising(int i) { int j = 1; bool flag = true; while (i > j&&flag) { if (g[i][j] == 1 && color[i] == color[j]) //가지치기 조건. 인접했고, 색깔이 같을 경우 { //return 0; 바로 종료하면 안됨 끝까지 탐색을 못함. 한번이라도 if문을 들어가면 칠하면안되는거니까 flag에 0을 넣어줌. flag = false; } j++; } return flag; } void draw(int i,int m , int &opt) { if (promising(i))//적절하면 실행하고 적절하지 않으면 넘어감. { if (i == N) //끝까지 다 칠했을 때 { cnt++; opt = 1; } else { for (int j = 1; j <=m; j++) //지정해준 m까지 반복문을 돌림 { color[i+1] = j; //i+1 에 j를 칠하고 draw(i+1)호출했는데 적절하지 않으면 다시 되돌아와서 다음색깔을 칠해줌. draw(i+1,m,opt); //다음칸에 칠하고 적절한지 검사함. } } } }
점점 Backtracking을 연습하니 점점 익숙해지는 느낌이 든다. 가지치기 조건과 재귀만 잘 생각하면 쉽게 풀 수 있는 문제였다.
'Skils > Algorithm' 카테고리의 다른 글
| 알고리즘[C++] 0-1 knapsack with 동적계획법(Dynamic programming) (0) | 2022.05.22 |
|---|---|
| 알고리즘[C++]-Hamiltonian Problem(해밀턴 회로 문제) (2) | 2022.05.16 |
| 알고리즘[C++]- Backtracking을 이용한 부분집합의 합(subset_sum)순서쌍 구하기. (0) | 2022.05.15 |
| [C++]-백트래킹(Backtracking)이란? + n-Queens문제 (0) | 2022.05.06 |
| 알고리즘[C++] - 허프만 코드(Huffman Code ) (0) | 2022.05.01 |
