📕Addition
- 덧셈을 할 때 digits들은 같은 자리에 bit들끼리 더해주는데 만약 더해서 2가 된다면 그 자리를 0으로 만들고 다음 자리에 1을 carry 해준다.
- 덧셈에 기본 방향은 오른쪽에서 왼쪽으로 넘어간다.
- 예를 들어서 7+6을 할 때
00000000 00000000 00000000 00000111 (2) = 7 (10)
+ 00000000 00000000 00000000 00000110 (2) = 6 (10)
= 00000000 00000000 00000000 00001101 (2) = 13 (10)
📕Subtraction
- 뺄셈은 덧셈을 사용해서 표현할 수도 있다.
- 더하고자 하는 수를 음수로 바꾼 뒤 더하면 간단하다.
- ex) 7 -6 = 7 + (-6) 이랑 같은 결과가 나온다.
따라서 우리는 2의 보수의 개념을 이용해서 6을 음수로 바꾸고 두 수를 더한다.
음수로 바꾸는 방법은 6을 ~6 + 1 해주면 된다.
📗덧셈을 사용하지 않고 빼는 경우
00000000 00000000 00000000 00000111 (2) = 7 (10)
- 00000000 00000000 00000000 00000110 (2) = 6 (10)
= 00000000 00000000 00000000 00000001 (2) = 1 (10)
📗2의 보수의 개념을 이용해서 음수로 바꾼 뒤 더해주는 경우
00000000 00000000 00000000 00000111 (2) = 7 (10)
+ 11111111 11111111 11111111 11111010 (2) = -6 (10)
= 00000000 00000000 00000000 00000001 (2) = 1 (10)
📕Overflow
- 오버플로우는 하드웨어가 표현할 수 없는 범위의 결과가 나올 때 발생한다.
- 몇가지 경우의 수가 있다.
- 양수 + 양수 = 음수
- 양수 - 음수 = 음수
- 음수 + 음수 = 양수
- 음수 - 양수 = 양수
📗오버플로우가 일어나지 않는 경우
- 부호가 다른 두 수를 더할 때 발생하지 않는다.
- 왜냐하면 두 개의 다른 부호의 수를 더한 결괏값은 더해지는 양수의 값보다 무조건 작기 때문에 오버플로우가 일어나지 않는다.
- ex) -10 + 4 = -6 에서 -6이라는 결과는 무조건 -10과 4 사이에 있기 때문에 오버플로우가 발생할 수 없다.
- 같은 부호의 두 수를 빼도 오버플로우는 일어나지 않는다.
- ex) c - a = c+ -a -> 위에 언급한 case인 두 개의 다른 부호의 수를 더하는 연산과 동일하기에 오버플로우가 발생하지 않는다.
- 왜냐하면 두 개의 다른 부호의 수를 더한 결괏값은 더해지는 양수의 값보다 무조건 작기 때문에 오버플로우가 일어나지 않는다.
📕Overflow Detection
- 두 개의 32-bit 수를 더하거나 뺄 때 33bit를 전부 다 사용하는 결과값을 표현해야 하는 경우가 있을 것이다.
- 그때 부호 비트는 계산 결과의 적절한 부호 대신 결과의 값으로 설정한다.
- 뺄셈에서 오버플로우가 일어나는 경우
- 양수 - 음수 = 음수
- 음수 - 양수 = 양수

📕Overflow Handling
- 부호가 없는 정수는 오버플로우를 무시하기 때문에 메모리 주소를 나타날 때 사용된다.
- 덧셈에서 합이 각각의 값보다 작은 경우에 오버플로우 발생한 것.
- ex) A+B = S 일 때 S <A or S <B인 경우
- 뺄셈에서 값이 빼지는 수보다 클 경우 오버플로우가 발생한 것.
- ex) A-B = S일때 S> A인 경우
- 덧셈에서 합이 각각의 값보다 작은 경우에 오버플로우 발생한 것.
- 컴퓨터 설계자들은 arithmetci overflow를 잘 다뤄서 해결해야 한다.
- C/C++ and java는 정수 오버플로우를 무시한다.
- 오버플로우를 다루는 것은 프로그래머들에게 매우 중요하다~!@?!#!@#!$~@$!
📕Multiplication by Hand
- Multiplying 1000 by 1001

여기서 product의 최대 길이는 length of multiplicand + length of multiplier이다.
- binary digits일 때, 각 곱셈의 과정의 결과는 매우 간단하다.
- multiplier의 bit가 1일 때 그대로 multiplicand를 복사한다.
- multiplier의 bit가 0일 때 0을 복사한다.
📕Sequential Version of the Multiplication
- 하드웨어 곱셈의 초기 버전
- 32-bit multiplier and 64-bit product registers
- 64-bit multiplicand register
- 64-bit ALU (Arithmetic and Logic Unit)
- Test-and-ADD-and-Shift
📗Exapmple of the Multiplication
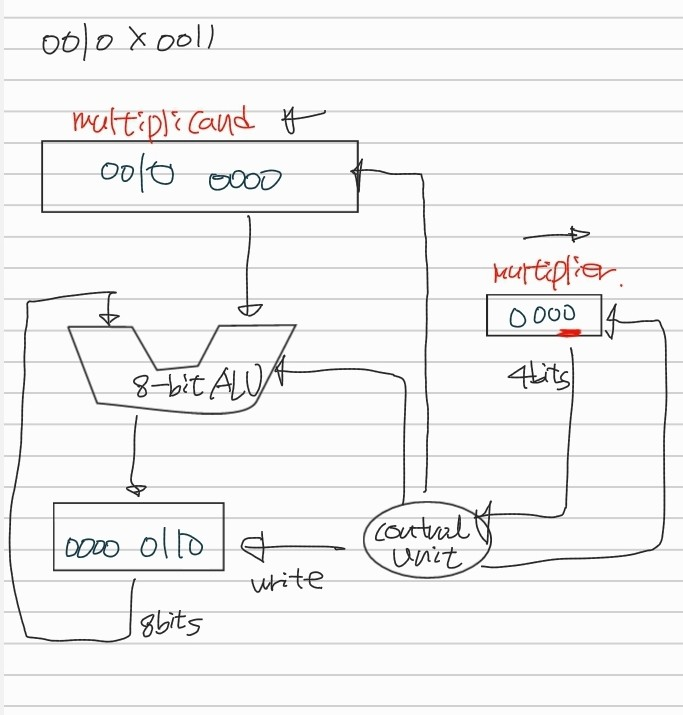
- 0011 X 0011
- multiplier의 LSB를 check 하고 그 값이 1이라면 더한다. 0이라면 그냥 넘어감.
- multiplicand register를 왼쪽으로 1bit shift 한다.
- multiplier를 오른쪽으로 1bit shift 한다.
- 이해하기 쉽게 각 과정을 그림으로 해보겠다.

- multiplier의 맨 오른쪽 bit인 LSB를 체크한다.
- 1이라면? multiplicand를 그대로 복사한다.
- 0이라면 0을 복사한다.
- multiplicand를 왼쪽으로 1 bit shift
- multilplier를 오른쪽으로 1 bit shift
- 이 과정이 주요 과정이다.
- 자릿수만큼 반복하면 계산을 끝낸다.



📕최적화 버전의 곱셈
- 하드웨어의 곱셈을 재정의
- 32-bit multiplicand register & 32-ALU (64->32bit)
- multiplier register (32->0) and 64-bit product register
- Multiplier는 64-bit product 레지스터의 절반을 기준으로 오른쪽에 위치한다.
- product의 왼쪽 절반에 곱셈을 더하고 결과를 product의 왼쪽 절반에 놓는다.
- multiplicand 대신에 product를 이동한다.

📗example of multiplication
- 0010 X 0011
- multiplier의 LSB가 1이라면 multiplicand를 더한다.
- product register를 오른쪽으로 1bit 이동시킨다.

- product의 오른쪽이 multiplier가 들어있다. LSB를 검사한다.
- 1이라면 multiplicand를 product의 왼쪽 부분에 더해준다.
- 0이라면 넘어간다.
- 더해주면 product에는 0010 0011이 들어가게 되는데 그다음 product에 전체 수를 오른쪽으로 1bit shift 한다.
- 그러면 product에는 0001 0001이 들어가게 된다
- 이러한 과정을 계속 반복한다.

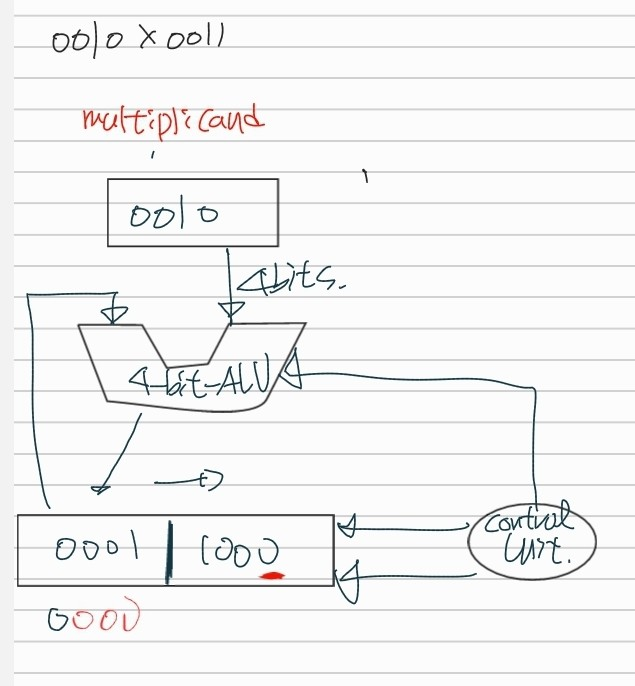


마지막 사진에 product에 있는 0000 0110이 최종 결과이다.
- 부호가 있는 곱셈은 어떻게 진행될까?
- multiplier와 multiplicand를 모두 양수로 바꿔준다.
- 31번 반복하는 동안 부호를 계산에서 제외한다.
- 만약 결과가 원래 부호와 다르다면 그것을 부정한다.
- 즉 부호를 무시하고 계산 후 마지막에 부호를 생각해준다.
📕Multiplications in RISC -V
- RISC -V는 곱셈을 위해 4가지의 인스트럭션을 가지고, signed or unsigned 64-bit product를 생산한다.
- mul (multiply) : integer 32-bit product를 생산함.
- mulh (mul high) : 두 연산자가 부호가 있다면 upper 32 bits of the 64-bit product를 생산함.
- mulhu (mulh unsigned) : 두 연산자가 부호가 없다면 upper 32 bits를 생산함.
- mulhsu (mulh sigend-unsigned) : 하나는 부호가 있고, 다른 하나가 부호가 없다면 upper 32-bit를 생산.
📗example
- upper부분은 경우에 따라 다르지만 lower부분은 항상 같다.
| Mode | A | B | AXB | Upper | Lower |
| Unsigned | 5(101) | 5(101) | 25(011001) | 011 | 001 |
| Signed | -3(101) | -3(101) | 9(001001) | 001 | 001 |
| Signed-Unsigned | 5(101) | -3(101) | -15(110001) | 110 | 001 |
mode에 따라 Upper 부분의 결과는 다르지만 lower 부분의 결과는 항상 같다.
📕Division by Hand
- 1001010 by 1000

Dividend = Quotient X Divisor + Remainder
- 이진법에서 나눗셈은 각 시도에 대한 몫의 자릿수를 만드는 것이다
- 0으로 나누는 것은 수학적으로 오류다.
- 따라서 divisors는 0이 될 수 없다.
📕Divison Algorithm and Hardware
- 하드웨어 나누기의 초기 버전
- 초기 곱셉의 버전과 같다.
- 다른 것은 shift 방향이다.
- 덧셈 대신에 뺄셈을 사용한다.
- Subtract-and-Test-and-Shift

📗example
- 0000 0111 % 0010
- 우선 divisor를 8bit로 확장한다. 0010 -> 0010 0000
- divisor를 remainder에 있는 값과 뺀다.
- 여기서 뺀 값의 MSB를 체크한다.
- 1이라면 음수가 나오기 때문에 적절한 연산이 아니므로 다시 더해줘서 restore 해준다.
- 0이라면 양수기 때문에 적절한 연산이므로 몫에 LSB에 1을 넣어준다. 0001
- 여기서 뺀 값의 MSB를 체크한다.
- divisor를 remainder에 있는 값과 뺀다.
- divisor를 오른쪽으로 1비트 이동시키고, 몫을 1비트 왼쪽으로 이동시킨다.
- divisor -> 0001 0000, quiotent -> 0010
- 위의 1,2,3 단계를 반복함
- 우선 divisor를 8bit로 확장한다. 0010 -> 0010 0000


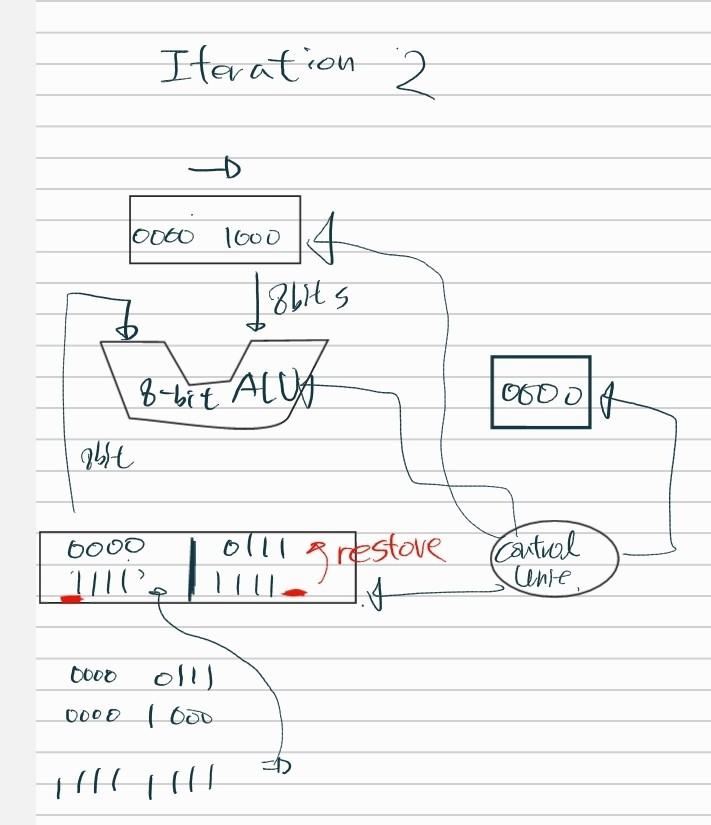

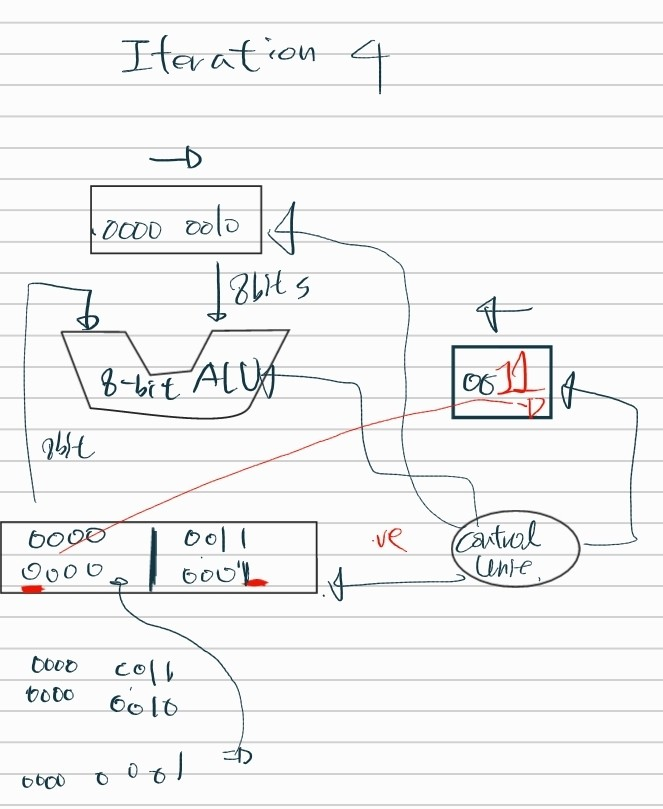
만약 restore가 아니고 양의 결과가 나왔다면 그 값이 고스란히 다시 remainder 블록에 들어가게 된다.
📕나누기의 최적화된 버전
- 나눗셈 하드웨어의 재정의
- 최적화된 곱셈의 하드웨어와 구조가 동일함.
- 왼쪽 오른쪽 둘 다 이동함.
- 덧셈 대신 뺄셈을 이용

- 0000 0111 % 0010
- 리마인더 레지스터에 왼쪽 4bit에서 divisor를 빼고 , sign bit를 check 한다.
- sign bit가 1이라면 restroe 하고, 리마인더 레지스터를 왼쪽으로 shift 한다.
- sign bit가 0이라면 왼쪽으로 1bit shift후 , 맨 오른쪽 bit를 1로 설정함.
- 모든 과정이 마친 뒤에 왼쪽으로 한 칸 밀어줌.
- 리마인더 레지스터에 왼쪽 4bit에서 divisor를 빼고 , sign bit를 check 한다.

- 0번째
- remainder의 half left - 0010의 결과를 check
- sign bit -> 1이라면 restore
- remainder를 왼쪽으로 1 shift
- remainder : 0000 1110
- remainder의 half left - 0010의 결과를 check
- 1번째
- remainder의 half left - 0010의 결과를 check
- sign bit -> 1이기에 restore
- remainder를 왼쪽으로 1 shift
- remainer : 0001 1100
- remainder의 half left - 0010의 결과를 check
- 2번째
- remainder의 half left - 0010의 결과를 check
- sign bit -> 1이기에 restore
- remainder를 왼쪽으로 1 shift
- remainder : 0011 1000
- remainder의 half left - 0010의 결과를 check
- 3번째
- remainder의 half left - 0010의 결과를 check
- sign bit -> 0이기에 remainder의 half left - 0010의 결과에다가 오른쪽 비트에 1을 붙여줌.
- remainder를 왼쪽으로 1 shift
- remainder : 0011 0001
- remainder의 half left - 0010의 결과를 check
- 4번째
- remainder의 half left- 0010의 결과를 check
- sign-bit가 0이기에 remainder의 half left - 0010의 결과에다가 오른쪽에 1을 붙여줌.
- remainder를 왼쪽으로 1 shift
- remainder : 0010 0011
- 계산을 진행하면서 왼쪽으로 5 shift 했다는 뜻은 지금 현재 몫의 bit가 5bit, 나머지의 bit가 3 비트라는 소리다.
- 우리는 몫 4bit, 나머지 4bit를 맞춰줘야 하기에, 한 칸 침범한 몫의 자리를 밀어낸다.
- remainder 레지스터에는 0001 0011이 저장되고, 왼쪽은 나머지, 오른쪽은 몫으로 들어가게 된다.
- 즉 Remainder : 0001 , Quotient : 0011
- remainder의 half left- 0010의 결과를 check
📕Signed division
- divisior과 dividend의 sigh-bit를 기억해서 계산 결과의 sign -bit가 적절하지 않는다면 negate 하면 된다.
- divison의 부호는 remainder의 부호와 동일하다.
- ex
- -7 % 2 -> Q=-3, R=-1 -> -3 * 2 -1 = -7 (O)
- -7 % 2 -> Q= -4 R=+1 -> -4*2 +1 = -7 (X)
- 나머지의 부호는 몫의 부호와 동일해야 한다!!
- 방법
- 부호의 계산을 무시하고 계산한다.
- 부호가 반대라면 몫을 negate 한다.
- 나머지의 부호를 몫의 부호와 일치시킨다.
📗RISC - V는 signed integers와 unsigned integers를 계산하기 위해 2가지의 divison 인스트럭션과 2가지 remainder 인스트럭션을 제공한다.
- div : divide
- divu : divide unsigned
- rem : remainder
- remu : remainder unsigned
📗shift for multiplication and divison
- 2를 곱한다 : shift left
- 2를 나눈다 : shift right
'Computer Science > Computer Architecture' 카테고리의 다른 글
| [Computer Architecture] - processor (1) (0) | 2022.10.23 |
|---|---|
| [Computer Architecutre] - floating point (0) | 2022.10.20 |
| [computer architecture]-instruction_language_of_computer(3) (0) | 2022.10.11 |
| [computer architecture]-instructions_language_of_computer(2) (0) | 2022.10.09 |
| [computer architecture] - instructions- language_of_computer(1) (1) | 2022.10.08 |
