📕Representing Numerical Data
📗Representing Negative Values
💡Signed-magnitue number representation : 부호-크기 표현
- 사람에 의해 사용됨
- 기존 숫자가 차지하는 bit 앞에 한자리의 bit를 더 사용한다.
- 0이면 양수 1이면 음수를 뜻한다.
- 예를 들어서 53의 2진수 표현은 0110101이다.
- +53은 기존 2진수인 0110101-> 00110101로 바꿔준다.
- -53은 기존 2진수인 0110101-> 10110101로 바꿔준다.
- 이러한 방식의 문제점은 0은 그냥 0이지만 +0과 -0이 존재한다는 점이다.
- 사람들에겐 아무 문제가 되지 않지만, 컴퓨터에
- 컴퓨터에겐 복잡하고 불필요한 문제이다.
- 해결방법
- 반으로 나눠서 표현한다. 예를 들어서 0~100까지 99까지 있다면 0~49는 양수를 뜻하고, 50~99는 음수를 뜻한다.
- 여기서 주의할 점은 50이 -1이 아니라 99가 -1이 되고 역순으로 숫자를 적어주면 된다.
- 컴퓨터 입장에서 매우 편한 방법
📗10의 보수(표현)

만약 k=2일 때 3의 보수를 구하고싶다면
100^2 - 3 = 97. 따라서 k가 2일때 3의 보수는 97이 된다.

두 방법 다 정확한 값이 나오지만 컴퓨터 입장에서는 보수의 개념이 계산하기 편하다.
98+96 = 194이지만 k가 2이기 때문에 2자리만 표현 가능하기 때문에 2자리를 제외한 숫자는 버림 한다.
보수의 개념에서 A-B = A+(-B)이다.
📗2의 보수
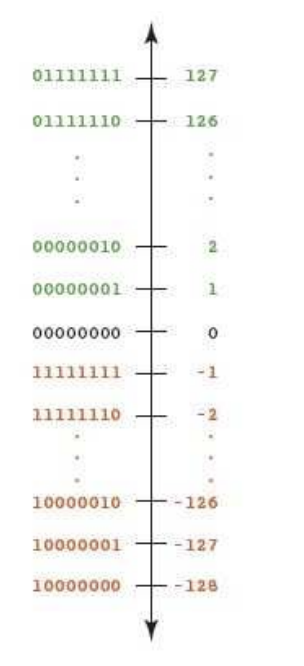
- 기본 수식
- neg(n) = 2^k -n
- neg(n)+n=2^k
- k가 8일 때
- 2^k=256 = (1 0000 0000)이다.
- -27의 2진수 표현
- neg(27)= 256-27
- neg(27)= (1 0000 0000)- (0001 1011)
- 1 + 255(1111 1111)-(0001 1011)
- 1+11100100
- 11100101
- 이렇게 하다 보니 놀라운 공식이 있다.
- 2의 보수는 그냥 0을 1로, 1을 0으로 바꾼 후 1을 더하면 된다.

10의 보수체계에서 -127+1 = -126이 성립한다.
하지만 2의 보수체계에서는 성립하지 않는다. (130이나 옴)
이러한 결과가 나오는 이유는 2^7은 128이지만 그 크기를 넘어서는 숫자를 표현하려고 해서 Overflow가 일어났다.
📗Number Overflow
8bit의 저장공간만을 사용할 때 127+3을 계산하면 overflow 발생
따라서 우리 컴퓨터는 32 bit 또는 64bit의 컴퓨터를 사용해서 overflow를 방지한다.
overflow의 확인 방법은 양수+양수를 더했는데 음수가 나온다면 -> overflow가 발생한 것.
📗실수 표현 방식
컴퓨터는 무한소수, 분수를 표현하기에 까다롭다.
따라서 자릿수가 제한된 수를 다룬다.

이러한 표현방식을 부동소수점이라고 한다.
과학적인 고나 점에서 컴퓨터로 12001.32708을 표현하려고 한다면 다음과 같은 방식을 약속했다.
1.200132708E+4 10^4를 곱한다는 뜻이다. E-3도 가능.
'학교 > 컴퓨터학개론' 카테고리의 다른 글
| [컴퓨터학개론 10장]- image &video (0) | 2022.07.03 |
|---|---|
| [컴퓨터학개론 9장]- Text & Audio (0) | 2022.07.03 |
| [컴퓨터학개론 7장]- Data & Computer (0) | 2022.06.29 |
| [컴퓨터학개론 6장]- binary number (0) | 2022.06.28 |
| [컴퓨터학개론 5장]- PC Architecture (0) | 2022.06.28 |
