문제
https://www.acmicpc.net/problem/2352
2352번: 반도체 설계
첫째 줄에 정수 n(1 ≤ n ≤ 40,000)이 주어진다. 다음 줄에는 차례로 1번 포트와 연결되어야 하는 포트 번호, 2번 포트와 연결되어야 하는 포트 번호, …, n번 포트와 연결되어야 하는 포트 번호가 주
www.acmicpc.net
문제 풀이
백준 문제를 자주 풀면 접해봤을 유형의 문제이다.
해당 문제의 유형은 LIS로 최장 증가 부분 수열의 길이를 구하는 문제이다.
왜냐하면 반도체의 선이 꼬이지 않게 가장 길게 연결하기 위해선 뒤에 등장하는 번호가 앞에 등장했던 번호들보다 커지면 안 되고,
이는 항상 앞에 등장했던 번호들보다 뒤에 등장하는 번호들이 작아짐이 보장되는 가장 긴 구간을 구해야 하기 때문이다.
여기서 조금 더 난이도가 길어진다면, 최장 부분 수열의 정확한 구간을 구하는 문제로 발전하지만, 해당 문제는 단순하게 구간의 길이를 구하면 된다.
LIS 문제에선 이분탐색 알고리즘을 통해 숫자가 들어갈 수 있는 위치를 계산할 수 있다.
문제의 전반적인 흐름은 다음과 같다.
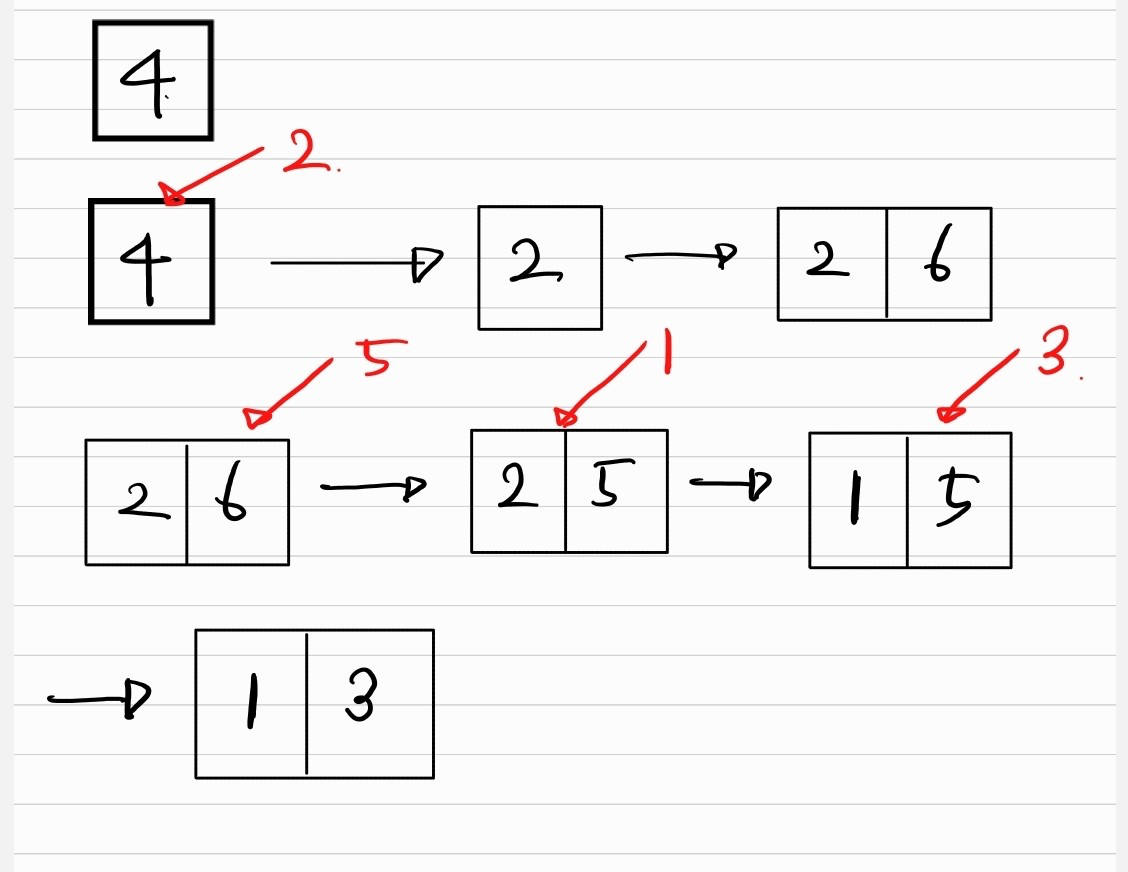
- 수열의 맨 뒤 원소보다 큰 원소는 그대로 구간에 붙여준다.
- 하지만 수열의 맨 뒤 원소보다 작은 원소가 등장한다면, 해당 원소가 들어갈 수 있는 위치를 찾아줘야 한다.
(여기서 이분탐색을 통해서 위치를 찾아준다) - n까지 반복하고, 수열의 크기가 가장 길게 증가하는 구간의 길이가 된다.
이분탐색에 대해 알아보자.
수열[mid]의 값과 내가 넣고자 하는 값(number)을 비교하면서, 범위 조절은 다음과 같은 규칙을 따른다.
- 수열[mid] > number : right를 mid-1로 조정해서, 탐색하려는 구간을 감소시킨다.
- 수열[mid] < number : left를 mid+1로 조정해서, 탐색하려는 구간을 증가시킨다.
- 수열[mid] == number : 인 경우는 존재하지 않는다. (같은 원소가 없는 것이 보장되기 때문이다)
여기서 left를 반환해야 할지, right를 반환해야 할지 고민이 되었다.
그림을 통해서 살펴보자.
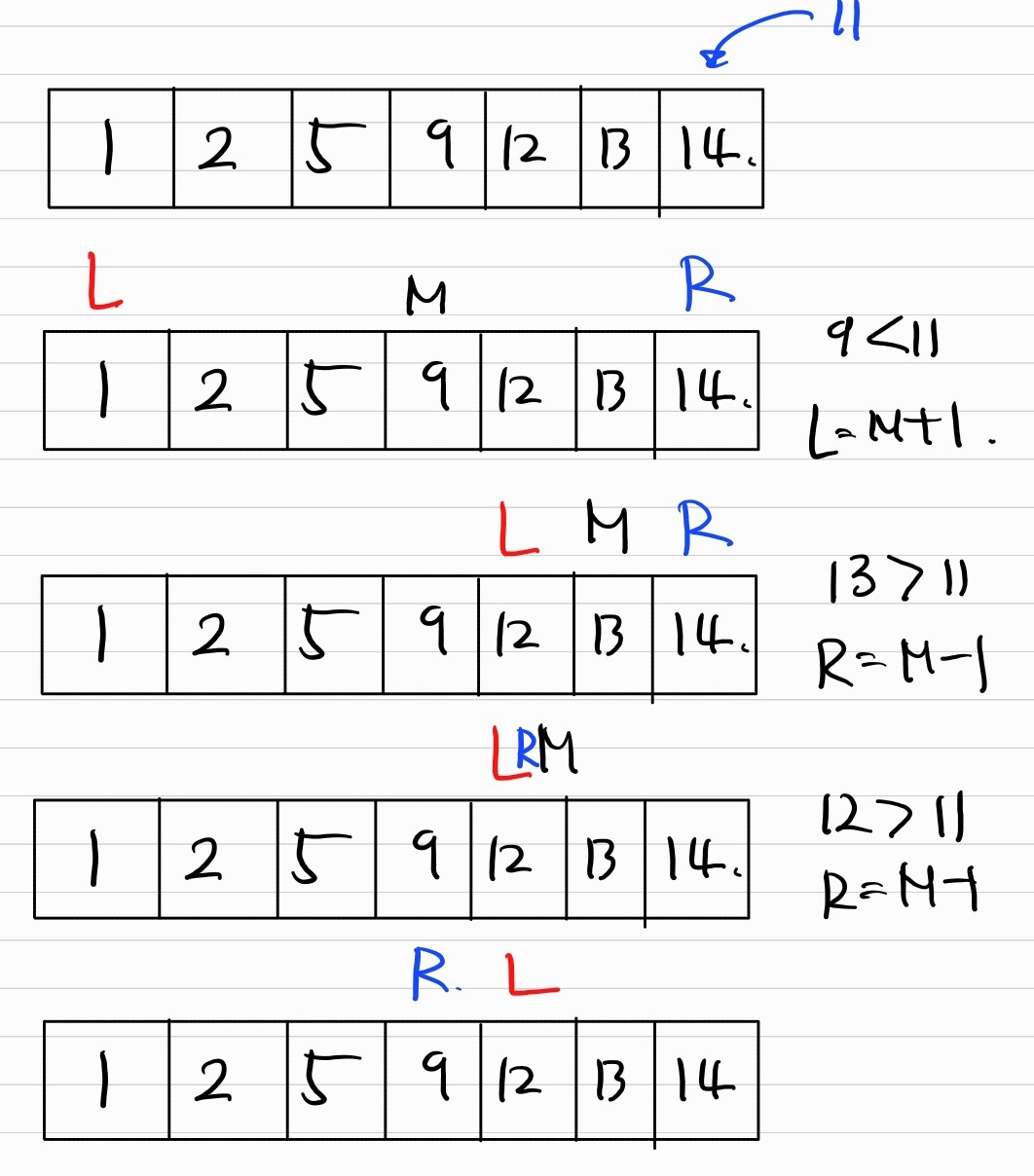
이분탐색이 끝나고 최종적인 R과 L의 위치는 다음과 같다.
11이 들어가야 할 위치는 R이 아닌 L임을 알 수 있고, 따라서 left를 반환하는 것이다.
전체 코드
class Solution {
private val br = System.`in`.bufferedReader()
private var n = 0
private lateinit var graph: IntArray
private val result = arrayListOf<Int>()
fun run() {
input()
solve()
print(result.size)
}
private fun input() {
n = br.readLine().toInt()
graph = br.readLine().split(" ").map { it.toInt() }.toIntArray()
}
private fun solve() {
result.add(graph.first())
for (i in 1 until n) {
if (result.last() < graph[i]) { //새로 들어오는 원소가 더 클 경우
result.add(graph[i])
} else { //더 작을 경우
val index = binarySearch(graph[i])
result[index] = graph[i]
}
}
}
private fun binarySearch(num: Int): Int { //num이 들어갈 수 있는 공간을 찾아야 함.
var left = 0
var right = result.size - 1
while (left <= right) {
val mid = (left + right) / 2
if (result[mid] > num) { //더 클 경우
right = mid - 1
} else { //작거나 같을 경우
left = mid + 1
}
}
return left
}
}
fun main() {
val solution = Solution().run()
}'CodingTest > Baekjoon' 카테고리의 다른 글
| [백준 16236] - 아기 상어(Kotlin)[골드3] (1) | 2024.04.21 |
|---|---|
| [백준 1766] - 문제집(Kotlin)[골드2] (1) | 2024.04.20 |
| [백준 1300] - k번째 수(Kotlin)[골드1] (2) | 2024.04.15 |
| [백준 1939] - 중량제한(Kotlin)[골드3] (0) | 2024.04.14 |
| [백준 1029] - 그림 교환(Kotlin)[골드1] (1) | 2024.04.10 |
문제
https://www.acmicpc.net/problem/2352
2352번: 반도체 설계
첫째 줄에 정수 n(1 ≤ n ≤ 40,000)이 주어진다. 다음 줄에는 차례로 1번 포트와 연결되어야 하는 포트 번호, 2번 포트와 연결되어야 하는 포트 번호, …, n번 포트와 연결되어야 하는 포트 번호가 주
www.acmicpc.net
문제 풀이
백준 문제를 자주 풀면 접해봤을 유형의 문제이다.
해당 문제의 유형은 LIS로 최장 증가 부분 수열의 길이를 구하는 문제이다.
왜냐하면 반도체의 선이 꼬이지 않게 가장 길게 연결하기 위해선 뒤에 등장하는 번호가 앞에 등장했던 번호들보다 커지면 안 되고,
이는 항상 앞에 등장했던 번호들보다 뒤에 등장하는 번호들이 작아짐이 보장되는 가장 긴 구간을 구해야 하기 때문이다.
여기서 조금 더 난이도가 길어진다면, 최장 부분 수열의 정확한 구간을 구하는 문제로 발전하지만, 해당 문제는 단순하게 구간의 길이를 구하면 된다.
LIS 문제에선 이분탐색 알고리즘을 통해 숫자가 들어갈 수 있는 위치를 계산할 수 있다.
문제의 전반적인 흐름은 다음과 같다.
- 수열의 맨 뒤 원소보다 큰 원소는 그대로 구간에 붙여준다.
- 하지만 수열의 맨 뒤 원소보다 작은 원소가 등장한다면, 해당 원소가 들어갈 수 있는 위치를 찾아줘야 한다.
(여기서 이분탐색을 통해서 위치를 찾아준다) - n까지 반복하고, 수열의 크기가 가장 길게 증가하는 구간의 길이가 된다.

이분탐색에 대해 알아보자.
수열[mid]의 값과 내가 넣고자 하는 값(number)을 비교하면서, 범위 조절은 다음과 같은 규칙을 따른다.
- 수열[mid] > number : right를 mid-1로 조정해서, 탐색하려는 구간을 감소시킨다.
- 수열[mid] < number : left를 mid+1로 조정해서, 탐색하려는 구간을 증가시킨다.
- 수열[mid] == number : 인 경우는 존재하지 않는다. (같은 원소가 없는 것이 보장되기 때문이다)
여기서 left를 반환해야 할지, right를 반환해야 할지 고민이 되었다.
그림을 통해서 살펴보자.

이분탐색이 끝나고 최종적인 R과 L의 위치는 다음과 같다.
11이 들어가야 할 위치는 R이 아닌 L임을 알 수 있고, 따라서 left를 반환하는 것이다.
전체 코드
class Solution { private val br = System.`in`.bufferedReader() private var n = 0 private lateinit var graph: IntArray private val result = arrayListOf<Int>() fun run() { input() solve() print(result.size) } private fun input() { n = br.readLine().toInt() graph = br.readLine().split(" ").map { it.toInt() }.toIntArray() } private fun solve() { result.add(graph.first()) for (i in 1 until n) { if (result.last() < graph[i]) { //새로 들어오는 원소가 더 클 경우 result.add(graph[i]) } else { //더 작을 경우 val index = binarySearch(graph[i]) result[index] = graph[i] } } } private fun binarySearch(num: Int): Int { //num이 들어갈 수 있는 공간을 찾아야 함. var left = 0 var right = result.size - 1 while (left <= right) { val mid = (left + right) / 2 if (result[mid] > num) { //더 클 경우 right = mid - 1 } else { //작거나 같을 경우 left = mid + 1 } } return left } } fun main() { val solution = Solution().run() }
'CodingTest > Baekjoon' 카테고리의 다른 글
| [백준 16236] - 아기 상어(Kotlin)[골드3] (1) | 2024.04.21 |
|---|---|
| [백준 1766] - 문제집(Kotlin)[골드2] (1) | 2024.04.20 |
| [백준 1300] - k번째 수(Kotlin)[골드1] (2) | 2024.04.15 |
| [백준 1939] - 중량제한(Kotlin)[골드3] (0) | 2024.04.14 |
| [백준 1029] - 그림 교환(Kotlin)[골드1] (1) | 2024.04.10 |

