문제
https://www.acmicpc.net/problem/14003
14003번: 가장 긴 증가하는 부분 수열 5
첫째 줄에 수열 A의 크기 N (1 ≤ N ≤ 1,000,000)이 주어진다. 둘째 줄에는 수열 A를 이루고 있는 Ai가 주어진다. (-1,000,000,000 ≤ Ai ≤ 1,000,000,000)
www.acmicpc.net
문제 풀이
가장 긴 증가하는 부분 수열 문제는 알고리즘의 명칭이 있을 정도로 유명한 문제이다.
DP를 이용해서 그 수열의 길이를 구한 문제는 풀어본 적이 있지만,
수열의 길이와 그 수열을 구해야 하는 문제는 따져줘야할것이 많기 때문에 DP로 풀면 안 될 거 같은 느낌이 왔다.
기존의 LIS 문제는 N의 크기가 크지 않아서 N^2 알고리즘으로 DP 배열을 계속 업데이트해서 풀 수 있었지만,
이번 문제는 N의 크기가 굉장히 커서 최대 nlogn으로 풀어야 했다.
nlogn 의 시간복잡도로 문제를 풀려고 하니 조금은 막막했다.
이래서 플레5인가 싶기도 하고.. ㅎ
아무튼 내가 했던 고민은 다음과 같다.
💡N^2은 안되니 한 번의 탐색으로 끝내야 한다.
예를 들어 10,20,10,30,20,50이 있다고 가정할 때 우리는 nlogn 알고리즘으로 문제를 해결해야 한다.
그렇다면 배열을 탐색하는데 n , 해당 숫자의 적당한 위치를 찾는데 logn이라는 결론이 나온다.
대표적인 logn 으로 위치를 찾는 알고리즘은 이분탐색이 있다.
하지만 내가 알던 이분탐색은 해당 인덱스의 정확한 위치를 반환해 주는 걸로 알고 있었기 때문에 조금은 변형이 필요했다.
즉 최적의 위치를 반환하는 이분탐색이 필요하다.
이분탐색으로 항상 숫자가 들어갈 수 있는 최적의 위치를 찾아준다.
하지만 이러한 수열은 올바른 수열이라고 할 수없다.
예를 들어서 설명해보면
1, 3, 1, 4, 2, 5라는 수열 A가 있고, 만들려는 수열은 B라고 가정하자.
우리는 이분탐색으로 인해 해당 숫자가 B에 들어갈 수 있는 위치를 찾을 수 있다.
당연하게도 B의 마지막보다 큰 숫자라면 B뒤에 붙여주면 된다.
우리가 생각해야 하는 것은 B의 마지막보다 작은 경우이다.
해당 경우는 이분탐색으로 찾아줘야 한다.
1의 경우
B는 비어있기 때문에 그냥 들어갈 수 있다.
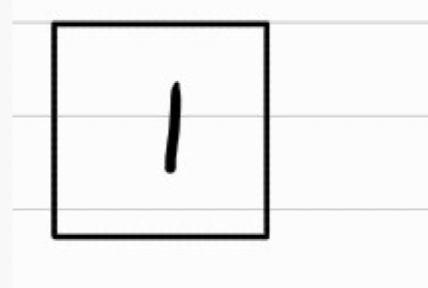
3과 4의 경우 B의 마지막인 1,3보다 크기 때문에 그냥 들어갈 수 있다.
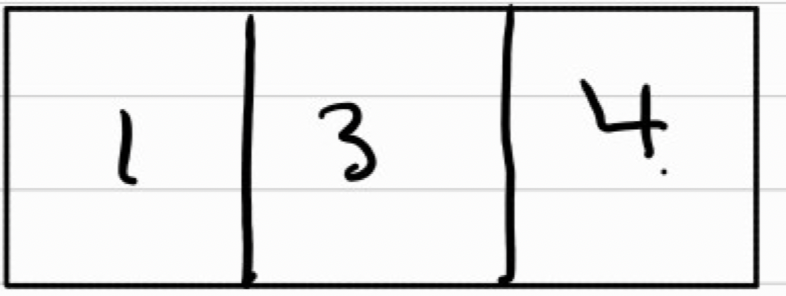
2의 경우 B의 마지막인 4보다 작기 때문에 이분탐색으로 위치를 찾아줘야 한다.
2가 들어갈 위치는 1 다음인 3의 위치가 될 것이다.

계속 명심해야 할 것은 우리는 이분탐색으로 숫자가 들어갈 위치를 찾는 것이지 끼워 넣는 것이 아니다.
마지막 5의 경우도 4보다 크기 때문에 B에 넣어준다.
최종 수열은 아래와 같다.

💡숫자의 길이를 보장할 뿐 정확한 수열은 아니었다.
하지만 해당 수열이 과연 옳은 수열일까? 아니다. 1,3,1,4,2,5를 가지고 1,2,4,5라는 수열은 만들 수가 없다.
길이는 같지만 정확한 수열이라고 할 수없다.
따라서 수열을 정확하게 추적하기 위해서 index 정보가 필요하다고 판단했다.
index 배열의 정의는 다음과 같다.
결과 배열에 위치한(혹은 했던) 위치값이다.
index 배열을 구하기 위해선 B배열에 넣은 후 해당 index를 기록하면 된다.
그렇다면 추가된 index 배열을 가지고 예를 살펴보자.
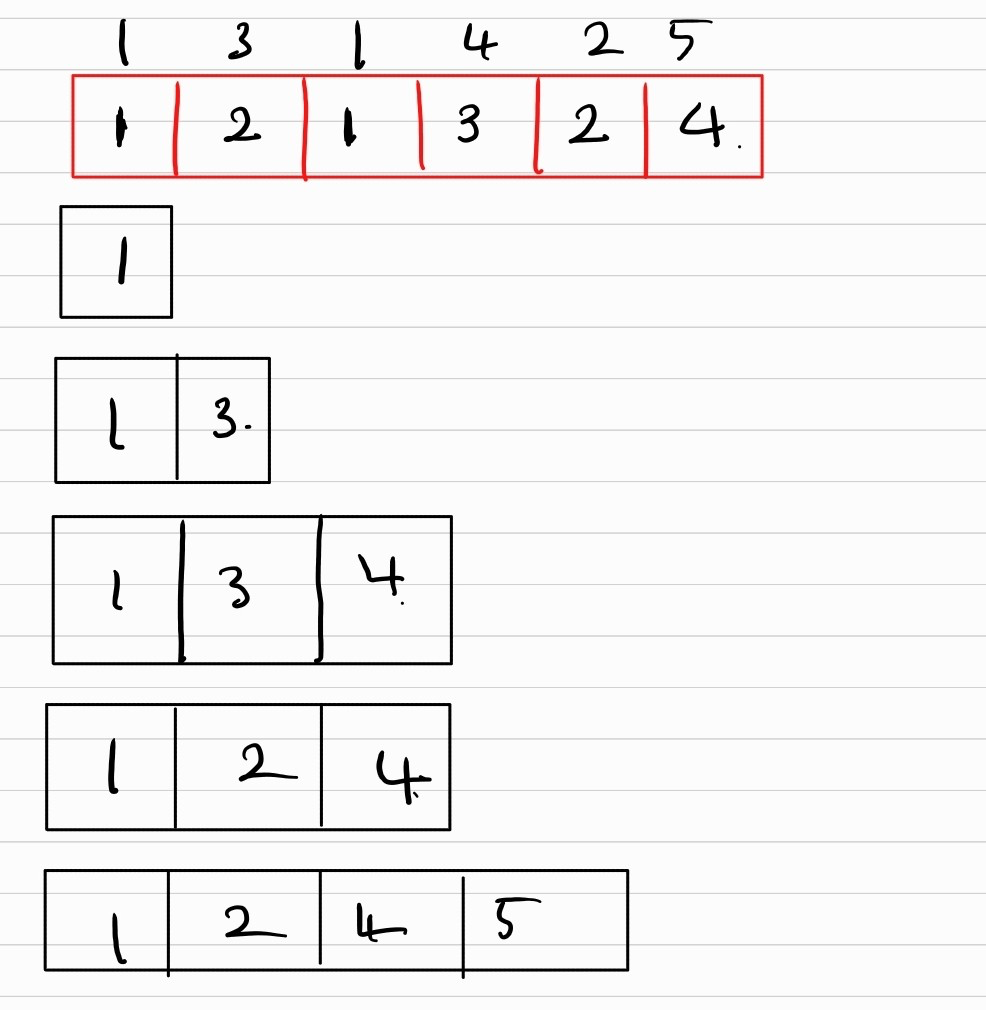
index 배열은 1,2,1,3,2,4이다.
1번 인덱스의 경우 후보는 1 하나이기 때문에 1이다.
나머지 3번과 4번의 경우도 후보는 하나이기 때문에 쉽게 정할 수 있다.
하지만 2번 인덱스의 경우 후보는 2와 3으로 2개이다.
그렇다면 어떻게 후보를 정할 수 있을까?
답은
자기보다 앞에 더 큰 인덱스에 해당하는 숫자가 등장했는지, 안 했는지이다.
이걸 판단하기 위해서는 배열의 뒤에서 접근하는 것이 효율적이다.
{1,2,1,3,2,4}라는 index 배열을 탐색할 때
index 배열의 4는 마지막이고 숫자는 5를 뜻한다.
그러면 우리는 index 배열의 3번을 연결해줘야 한다.
연결하기 전에 등장한 숫자들은 모두 의미가 없는 숫자이다.
따라서 index 배열에 4번에 있는 2가 무시되고, 3번이 연결되고, 그 앞에 있는 index값이 2인 숫자 3이 선택되는 것이다.
전체 코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.HashSet;
import java.util.List;
import java.util.StringTokenizer;
public class Main {
static BufferedReader br;
static StringTokenizer st;
static int n;
static int[] numbers;
static int[] idx;
static ArrayList<Integer> result;
static List<Integer> ary;
public static void main(String[] args) throws IOException {
input();
Solution();
findIdx();
StringBuilder sb = new StringBuilder();
sb.append(result.size()).append("\n");
for (int i = result.size() - 1; i >= 0; i--) {
sb.append(result.get(i)).append(" ");
}
System.out.println(sb);
}
public static void input() throws IOException {
br = new BufferedReader(new InputStreamReader(System.in));
st = new StringTokenizer(br.readLine());
n = Integer.parseInt(st.nextToken());
numbers = new int[n + 1];
idx = new int[n + 1];
ary = new ArrayList<>();
result = new ArrayList<>();
st = new StringTokenizer(br.readLine());
for (int i = 1; i <= n; i++) {
numbers[i] = Integer.parseInt(st.nextToken());
}
}
public static void Solution() {
ary.add(numbers[1]);
idx[1] = 1;
for (int i = 1; i <= n; i++) {
if (ary.get(ary.size() - 1) < numbers[i]) {
ary.add(numbers[i]);
idx[i] = ary.size() - 1;
} else { //아닐때는 넣을 위치를 찾아줘야 한다.
int numberIdx = binarySearch(i, 0, ary.size() - 1);
ary.set(numberIdx, numbers[i]);
idx[i] = numberIdx;
}
}
}
public static int binarySearch(int idx, int left, int right) {
int mid;
while (left < right) {
mid = (left + right) / 2;
if (numbers[idx] == ary.get(mid)) {
return mid;
}
if (numbers[idx] > ary.get(mid)) {
left = mid + 1;
} else {
right = mid;
}
}
return left;
}
public static void findIdx() { //나보다 idx값이 큰 녀석이 등장했는지 안했는지를 찾아야 함.
int index = ary.size() - 1;
for (int i = n; i >= 1; i--) {
if (index == idx[i]) {
result.add(numbers[i]);
index--;
}
}
}
}'CodingTest > Baekjoon' 카테고리의 다른 글
| [백준 1562] - 계단 수(JAVA)[골드1] (0) | 2024.03.03 |
|---|---|
| [백준 2568] - 전깃줄-2(JAVA)[플레5] (0) | 2024.03.02 |
| [백준 17143] - 낚시왕(JAVA)[골드1] (0) | 2024.02.15 |
| [백준 12100] - 2048(Easy) (JAVA)[골드2] (5) | 2024.02.13 |
| [백준 2098] - 외판원 순회(JAVA)[골드1] (0) | 2024.02.12 |
