문제
https://www.acmicpc.net/problem/16927
16927번: 배열 돌리기 2
크기가 N×M인 배열이 있을 때, 배열을 돌려보려고 한다. 배열은 다음과 같이 반시계 방향으로 돌려야 한다. A[1][1] ← A[1][2] ← A[1][3] ← A[1][4] ← A[1][5] ↓ ↑ A[2][1] A[2][2] ← A[2][3] ← A[2][4] A[2][5]
www.acmicpc.net
문제 풀이
정말 싫어하는 문제의 부류이다..
배열 회전, 뒤집기 같이 수학과 같이 사용해야 하는 문제는 정말 까다로운 것 같다.
해당 문제의 특이점은 배열 전체를 회전시키는것이회전시키는 것이 아닌 각 인덱스의 원소들을 회전시키는 것이다.
통째로 회전하는 것과 소용돌이처럼 회전시키는 것은 아예 다른 문제이다.
소용돌이식 회전을 위해서 어떻게 해야 할지 고민을 해봤다
n*n 반복문을 돌리면서 각 위치에 맞게 돌리기
사실상 불가능한 영역이라고 판단했다.
해줘야 할 연산도 굉장히 많고, 최대 300 크기의 배열을 식을 세워서 회전하는 것은 쉽지 않을 것이라고 생각했다.\
규칙을 찾기 위해서 무작정 손으로 그려봤다.
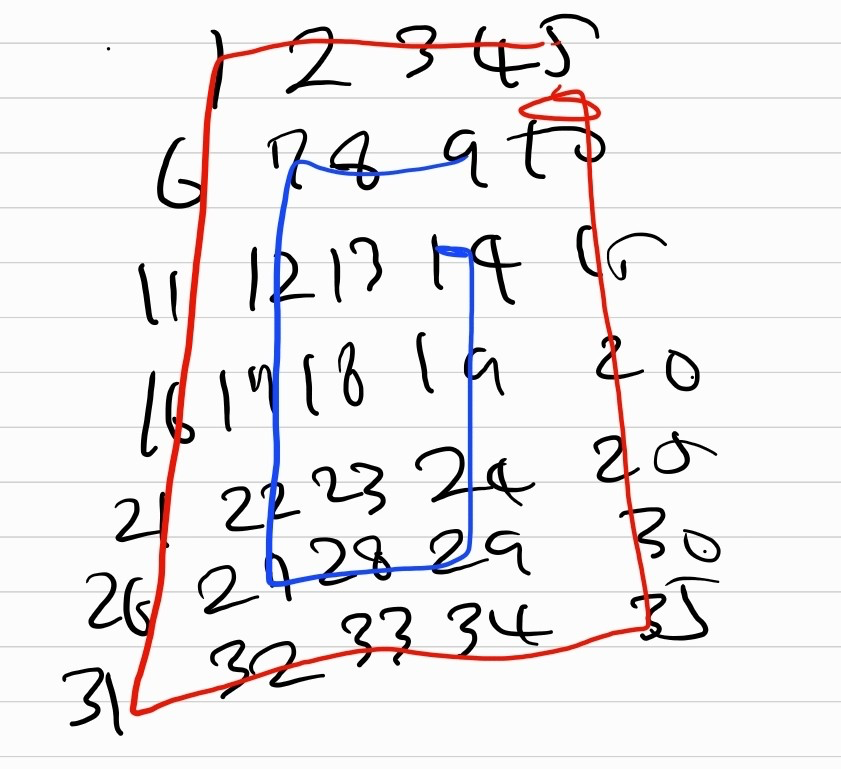
그림을 그리다 보니 규칙이 보였다.
규칙은 바로 사각형의 층마다 껍데기가 존재하고 같은 껍데기에 포함되어 있는 숫자들만 회전을 하는 것이었다.
depth에 맞는 껍데기에 원소들만 회전시키기
행렬과 회전의 특성만 기억한다면 , 껍데기의 개수는 간단하게 구할 수 있었다.
1 2 3 4
5 6 7 8
9 10 11 12
위 행렬은 행의 개수가 3, 열의 개수가 4인 행렬이다.
위 행렬의 껍데기 수는 1개이다.
즉 색깔로 칠해진 영역만 회전하는 것이다.
하나의 예를 더 들자면
1 2 3 4 5
5 4 3 2 1
7 8 1 2 3
3 4 6 9 5
7 1 2 3 4
1 2 3 4 5
위 행렬은 행의 개수가 6 열의 개수가 5인 행렬이다.
행렬의 껍데기 수는 2개이다.
즉 껍데기의 수는 행의 개수와 열의 개수 중 작은 것의 절반값이다.
이렇게 회전을 1번 할 때마다 껍데기들을 회전시켜 줬다.
회전 알고리즘은 구현하기 나름이므로 설명은 생략하겠다.
그 후 회전알고리즘을 적용해서 제출했더니 시간초과가 발생했다.

간과한 것이 있다면 회전의 수에도 규칙이 있고, 일정한 수의 회전을 진행하면 제자리로 돌아오는 규칙이 있다.
즉 회전의 수를 전부 다 할 필요가 없이, 규칙을 찾아야 한다는 것이다.
그러기 위해서 하나의 지점에서 얼마나 이동해야 제자리로 돌아오는지 계산했고, 규칙을 찾았다.
사각형의 전체 변의 길이에서 꼭짓점을 뺀 횟수만큼 회전을 할 경우 제자리로 돌아왔다.
이건 직접 해보면 알 수 있을 것이다. 꼭짓점을 뺀 이유는 꼭짓점에서 방향전환이 일어나기 때문에 횟수에서 빼주는 것이다.
이런 돌아오는 길이를 안다면 회전을 전부 다 할 필요 없이 회전% 길이의 값으로만 회전을 하면 똑같은 결과를 얻을 수 있다.
항상 문제를 잘 읽고.. 최악의 경우의 수까지 생각을 해야 하는데 쉽지가 않은 것 같다.ㅠ
전체 코드
import java.io.*;
import java.util.*;
public class Main {
static BufferedReader br;
static StringTokenizer st;
static int n;
static int m;
static int r;
static int[][] graph;
public static void main(String[] args) throws IOException {
br = new BufferedReader(new InputStreamReader(System.in));
input();
int newN = n;
int newM = m;
for (int i = 0; i < Math.min(n, m) / 2; i++) {
rotate(i, 2 * newN + 2 * newM - 4);
newN -= 2;
newM -= 2;
}
printGraph();
}
public static void input() throws IOException {
st = new StringTokenizer(br.readLine());
n = Integer.parseInt(st.nextToken());
m = Integer.parseInt(st.nextToken());
r = Integer.parseInt(st.nextToken());
graph = new int[n][m];
for (int i = 0; i < n; i++) {
st = new StringTokenizer(br.readLine(), " ");
for (int j = 0; j < m; j++) {
graph[i][j] = Integer.parseInt(st.nextToken());
}
}
}
public static void rotate(int start, int length) {
int number = r % length; //회전수
for (int i = 0; i < number; i++) {
Point p1 = new Point(start, start, graph[start][start]); //왼쪽 위
Point p2 = new Point(start, m - start - 1, graph[start][m - start - 1]); //오른쪽 위
Point p3 = new Point(n - start - 1, start, graph[n - start - 1][start]); //왼쪽 아래
Point p4 = new Point(n - start - 1, m - start - 1, graph[n - start - 1][m - start - 1]); //오른쪽 아래
//윗변 움직이기
for (int j = start; j < m - 1 - start; j++) {
graph[start][j] = graph[start][j + 1];
}
//왼쪽변 움직이기
for (int j = n - start - 1; j > start + 1; j--) {
graph[j][start] = graph[j - 1][start];
}
//아래변 움직이기
for (int j = m - 1 - start; j > start + 1; j--) {
graph[n - 1 - start][j] = graph[n - 1 - start][j - 1];
}
//오른쪽변 움직이기
for (int j = start; j < n - 1 - start; j++) {
graph[j][m - 1 - start] = graph[j + 1][m - 1 - start];
}
//각각의 꼭짓점 다시 넣어주기
graph[p1.x + 1][p1.y] = p1.v;
graph[p2.x][p2.y - 1] = p2.v;
graph[p3.x][p3.y + 1] = p3.v;
graph[p4.x - 1][p4.y] = p4.v;
}
}
public static void printGraph() {
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
System.out.print(graph[i][j] + " ");
}
System.out.println();
}
}
static class Point {
int x;
int y;
int v;
public Point(int x, int y, int v) {
this.x = x;
this.y = y;
this.v = v;
}
}
}'CodingTest > Baekjoon' 카테고리의 다른 글
| [백준 17406] - 배열돌리기4(JAVA)[골드4] (0) | 2024.01.19 |
|---|---|
| [백준 16935] - 배열 돌리기3(JAVA)[골드5] (0) | 2024.01.17 |
| [백준 17471] - 게리멘더링(JAVA)[골드4] (1) | 2024.01.15 |
| [백준 2887] - 행성터널(Java)[플레5] (0) | 2024.01.13 |
| [백준 10026] - 적록색약(Java)[골드5] (3) | 2024.01.13 |
