문제
https://school.programmers.co.kr/learn/courses/30/lessons/72413
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
문제 풀이
문제를 보자마자 떠올랐던 생각은 다익스트라..? 를 사용하는 것이라고 생각했다.
S에서 출발해서 A와 B가 가장 적게 낼 수 있는 택시비의 요금을 구해야 한다.
하지만 까다로운 점은 A와 B가 따로따로 타는 경우고 고려해서 정말 어려웠던 문제였던 거 같다.
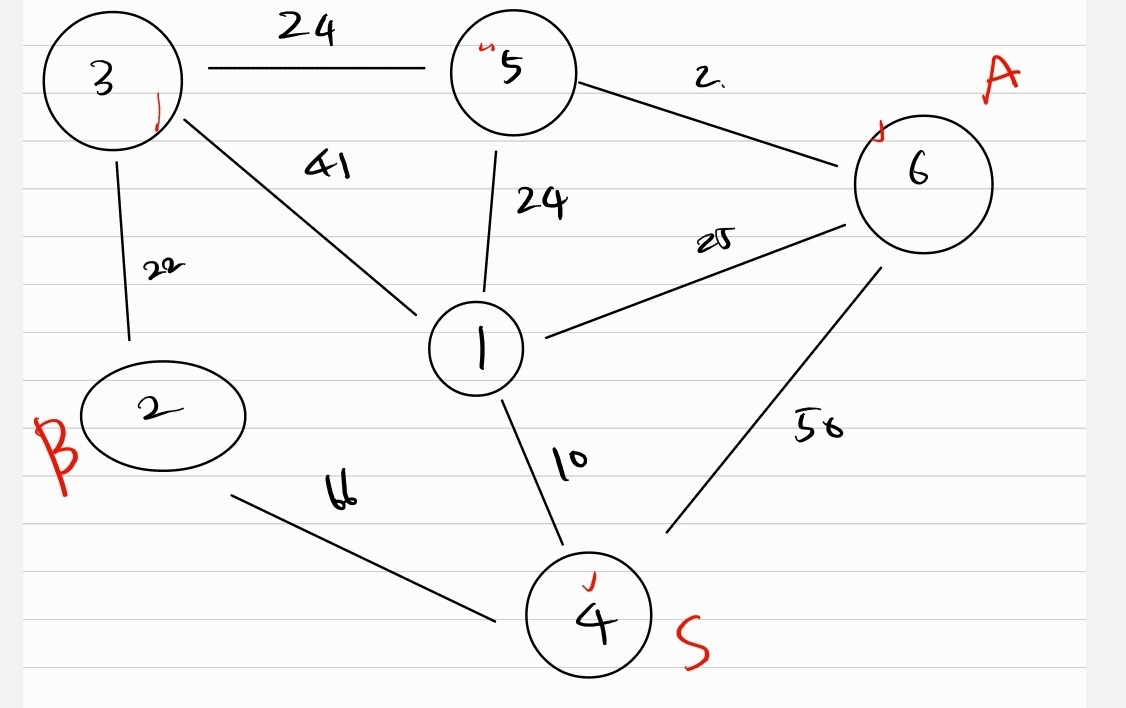
우선 나는 다익스트라 알고리즘을 통해서 정점마다 최소 거리를 구하려고 했다.
우선 A와 B가 따로따로 택시를 타는 경우는 S에서 B 최소경로, S에서 A까지의 최소경로를 구하면 되기 때문에 간단하고,
여기까지는 대부분 접근할 수 있을 것이다.
그다음이 문제다.
S에서 출발해서 어느 지점에서 택시를 갈아타야 A와 B가 최소비용으로 집에 도착할 수 있을까에 대한 여부를 결정해줘야 한다.

첫 번째로 접근한 방법은 A에서 B까지의 최단 경로를 구해서 해당 지점과 S를 연결하는 것이었다.
해당 경로에서 A와 B가 따로 택시를 타더라도 걸리는 비용은 48로 동일하다.
왜냐하면 해당 경로의 전체 비용은 48이기 때문에, 어디에서 택시를 갈아타더라도 비용은 48로 고정된다.
예를 들어서 3에서 택시를 갈아탄다면
- 3 -> B : 22 / 3 -> A : 24 -> 48
- 5 -> B : 46 / 5 -> A : 2 -> 48
- 2-> B : 0 / 2 -> A : 48
- 6 -> B : 48 / 6-> A : 48
즉 A와 B의 최단 경로를 거쳐가는 지점에서 택시를 갈아타면 48이라는 비용은 고정이다.
따라서 이 경로 중에서 S와 최단경로에 해당하는 지역을 찾아서 연결하면 된다.
- (S -> 5 : 34) + (5 -> A : 5) + (5 -> B : 48) --> 82
- (S -> 3 : 51) + (3 -> A : 24) + (3 -> B : 22) --> 97
- (S -> 2 : 66) + (2 -> A : 48) + (2 -> B : 0) --> 114
- (S -> 6 : 35) + (6 -> A : 0) + (6 -> B : 48) --> 83
하지만 이러한 방식은 A->B까지의 최단경로를 지나는 지점을 찾기 어려울 뿐만 아니라, 예외 케이스도 있었다.
아래가 그 예외 케이스이다.
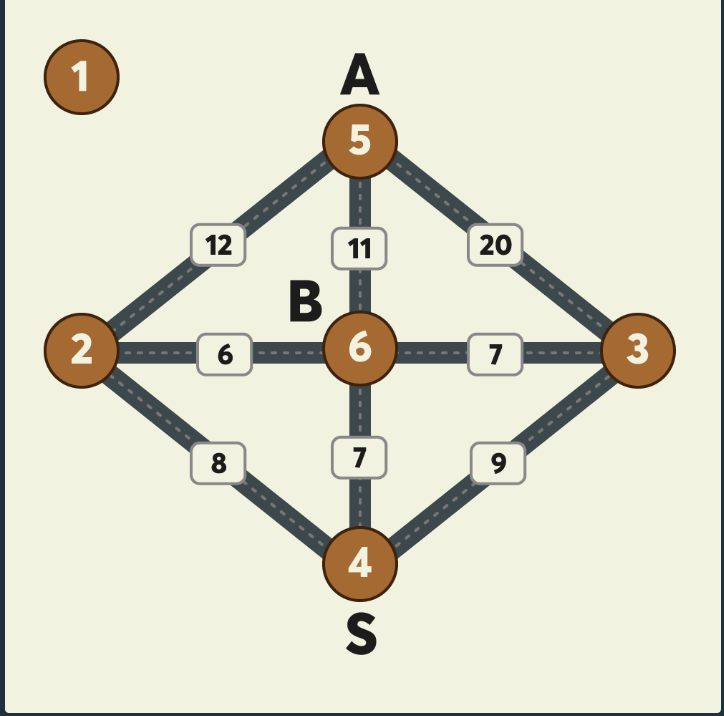
내가 생각한 알고리즘으로는 해당 그림에서 답을 구할 수가 없었다.
따라서 알고리즘을 수정했다.
A가 갈 수 있는 지점들까지의 최소 비용을 모두 구하고, B가 갈 수 있는 지점들까지의 최소비용을 모두 하고, S에서 갈 수 있는 모든 지점들까지의 최소 비용을 구해서 해당 지점들을 계산해서 최솟값을 계산하는 것이다.
위에서 내가 접근했던 방식과 유사하지만, 나는 더욱 최적화를 위해서 필요한 경로만 측정해 줬지만, 해당 방법은 너무 복잡했다.
따라서 위 알고리즘으로 수정했다.
위 알고리즘을 이용하면 간단하게 다익스트라 알고리즘을 3번 호출하고, 최솟값을 구할 수 있다.
해당 문제를 풀 때 플로이드 워셜 알고리즘을 사용한 경우도 있지만, 플로이드 워셜 알고리즘은 시간복잡도가 N^3이고, 해당 알고리즘은 N^3보단 적은 시간복잡도가 소요된다.
코드적으로는 간단하게 설명할 예정이다.
- makeGraph를 통해서 양방향으로 값들을 넣어준다.
- dijsktra함수는 인자로 받은 지점을 출발지점으로 인식하고 최소 비용을 구해준다.
- findMinNode는 출발지점에서 방문하지 않는 지점 중 가장 비용이 적은 지점을 찾아내서 반환한다.
- 그렇다면 해당 지점을 방문처리 해주고 거리를 update 해준다.
- 기존의 거리보다 다른 노드를 거치고 간 거리가 짧다면 업데이트시켜준다.
- 다익스트라 알고리즘을 실행하면 출발지점에서 모든 지점의 최소비용을 가지는 dist 배열이 반환된다.
- 이제 각 배열들을 비교해서 S->i, A->i, B->i의 비용이 최소비용인 경우를 찾고, 최소비용을 반환한다.
전체 코드
import kotlin.math.*
class Solution {
lateinit var graph: Array<Array<Int>>
lateinit var dist: Array<Int>
lateinit var visit: Array<Boolean>
var answer = 100000000
val INF = 100000000
fun solution(n: Int, s: Int, a: Int, b: Int, fares: Array<IntArray>): Int {
graph = Array(n + 1) { Array(n + 1) { INF } }
makeGraph(fares)
val distS = dijkstra(s)
val distA = dijkstra(a)
val distB = dijkstra(b)
for (i in 1 until n + 1) {
answer = min(answer, distS[i] + distA[i] + distB[i])
}
return answer
}
private fun makeGraph(fares: Array<IntArray>) {
for (input in fares) {
graph[input[0]][input[1]] = input[2]
graph[input[1]][input[0]] = input[2]
}
}
private fun dijkstra(from: Int): Array<Int> {
dist = Array(graph.size) { INF }
for (i in 1 until dist.size)
dist[i] = graph[from][i]
visit = Array(dist.size) { false }
visit[from] = true
dist[from] = 0
for (i in 1 until dist.size) {
val minNode = findMinNode()
visit[minNode] = true
update(minNode)
}
return dist
}
private fun update(minNode: Int) {
for (j in 1 until dist.size) {
if (dist[j] > dist[minNode] + graph[j][minNode]) {
dist[j] = dist[minNode] + graph[j][minNode]
}
}
}
private fun findMinNode(): Int {
var min = INF
var minIdx = 0
for (i in 1 until dist.size) {
if (visit[i]) continue
if (min > dist[i]) {
min = dist[i]
minIdx = i
}
}
return minIdx
}
}
'CodingTest > Programmers' 카테고리의 다른 글
| 프로그래머스[programmers] - 이모티콘 할인행사(Kotlin)[LV2] (2) | 2023.10.24 |
|---|---|
| 프로그래머스[programmers] - 양궁대회(Kotlin)[LV2] (2) | 2023.10.23 |
| 프로그래머스[programmers] - N으로 표현(Kotlin)[LV2] (1) | 2023.10.06 |
| 프로그래머스[programmers] - 네트워크(Kotlin)[LV3] (0) | 2023.09.23 |
| 프로그래머스[programmers] - 교점에 별 만들기(Kotlin)[LV2] (0) | 2023.09.17 |
