📕문제
https://www.acmicpc.net/problem/2533
2533번: 사회망 서비스(SNS)
첫 번째 줄에는 친구 관계 트리의 정점 개수 N이 주어진다. 단, 2 ≤ N ≤ 1,000,000이며, 각 정점은 1부터 N까지 일련번호로 표현된다. 두 번째 줄부터 N-1개의 줄에는 각 줄마다 친구 관계 트리의 에
www.acmicpc.net
🔎문제설명
모든 사회망 구성원들이 아이디어를 받아들일 수 있게끔 하기 위해 필요한 최소한의 얼리어답터의 개수를 구해야 한다.
A가 얼리어답터가 되기 위해서는, A의 친구들이 모두 얼리어답터여야 합니다.
즉 A와 연결된 모든 정점들이 얼리어답터여야합니다.
기본적인 DFS는 리프노드까지 진행한 후 과정을 진행하기에, 리프노드에서부터의 작업을 진행해야 합니다.
우선 저의 처음 접근방식은
내가 리프노드이고, 만약 부모가 얼리어답터가 아니라면, 그 부모를 얼리어답터로 만들어줬습니다.
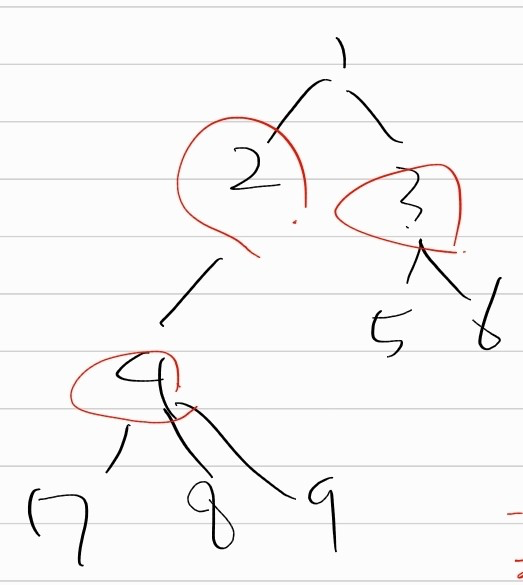
1번->2번->4번->7번을 방문하고, 7번이 리프노드이기에, 7번과 연결된 4번을 얼리어답터로 만들어줬습니다.
8번과 9번은 4번이 얼리어답터이면, 자신들도 얼리어답터의 조건을 충족하기에, 상관없습니다.
이런 식으로 리프노드를 타고 올라가서, 부모노드를 얼리어답터로 바꿔주는 작업을 했습니다.
이러한 방법이 결과적으로 얼리어답터의 숫자를 최소한으로 사용할 거라고 생각했습니다.
하지만 멸망했습니다..
조건이 너무 단순했던 걸까요..? 아니면 최소한의 얼리어답터의 수를 못 구했던 걸까요..
그래서 풀이방식을 수정했습니다.
질문게시판을 보니 대부분 DP를 섞어서 풀었더라고요. DP.. 생각도 못했습니다. ㅠㅠ
우선 DP 방식의 기본적인 접근방법은 다음과 같습니다.
DP [idx][0] : idx가 얼리어답터일 때, 해당 노드 + 자식 노드 중 만족하는 최소한의 얼리어답터의 수입니다.
DP [idx][1] : idx가 얼리어답터가 아닐 때, 해당 노드 + 자식 노드 중 만족하는 최소한의 얼리어답터 수입니다.
이러한 작업도 리프노드에서 부터 거꾸로 올라가기 때문에, 잘 생각해봐야 합니다.

💡그림 설명
- DP [7][0] =1, DP [7][1]=0입니다.
- 8,9도 동일합니다.
- DP [4][0]=1, DP [4][1]=3입니다.
- 4가 얼리어답터라면, 7,8,9는 얼리어답터일 필요성이 없기 때문에, DP [4][0]는 1이고,
- 4가 얼리어답터가 아닐 경우, 7,8,9 모두 얼리어답터여야 하기 때문에, DP [4][1]=3입니다.
- 이런 식으로 쭉쭉 진행하다가, 우리가 필요한 것은 DP [1][0]과 DP [1][1] 두 값 중 최솟값입니다.
- 계속해서 아래에서 더해준 값을 DP로 저장하는 메모이제이션 방법을 사용합니다.
💻전체 코드
#include <iostream>
#include <vector>
#include <algorithm>
#include <math.h>
using namespace std;
int n;
int answer = 0;
bool V[1000001];
vector<vector<int> >dp;
vector<int> graph[1000001];
void funct(int idx);
int main()
{
cin >> n; // n은 정점의 개수
int s, e;
dp.resize(n+1,vector<int>(2,0));
for (int i = 0; i < n - 1; i++)
{
cin >> s >> e;
graph[s].push_back(e); // s->e
graph[e].push_back(s); // e->s
}
funct(1);
answer=min(dp[1][0],dp[1][1]);
cout<<answer<<endl;
}
void funct(int idx){
V[idx]=true; //방문처리.
dp[idx][0]=1; //
for(int i=0; i<graph[idx].size();i++){
int next=graph[idx][i]; //다음 방문할 지역
if(V[next]) //방문한 지역이라면
continue;
funct(next);
dp[idx][0]+=min(dp[next][0], dp[next][1]); //idx가 얼리어답터일때
dp[idx][1]+=dp[next][0]; //idx가 얼리어답터가 아닐때
}
}
😀느낀 점
- 코드적으로는 굉장히 간단합니다.
- 접근방식이 트리 -> DP로 넘어가는 게 어려워서 골드 3이라는 난이도인 거 같습니다.
- 조건만 잘 이해한다면 그렇게 어려운 문제는 아니었습니다!
'CodingTest > Baekjoon' 카테고리의 다른 글
| [백준 14502] - 연구소(Kotlin)[골드4] (0) | 2023.08.10 |
|---|---|
| [백준 11967] - 불 켜기(C++)[골드2] (2) | 2023.07.05 |
| [백준 1967] - 트리의 지름(C++)[골드4] (1) | 2023.05.12 |
| [백준 9489] - 사촌(C++)[골드4] (1) | 2023.05.11 |
| [백준 21608] - 상어 초등학교(C++)[골드5] (0) | 2023.05.11 |
📕문제
https://www.acmicpc.net/problem/2533
2533번: 사회망 서비스(SNS)
첫 번째 줄에는 친구 관계 트리의 정점 개수 N이 주어진다. 단, 2 ≤ N ≤ 1,000,000이며, 각 정점은 1부터 N까지 일련번호로 표현된다. 두 번째 줄부터 N-1개의 줄에는 각 줄마다 친구 관계 트리의 에
www.acmicpc.net
🔎문제설명
모든 사회망 구성원들이 아이디어를 받아들일 수 있게끔 하기 위해 필요한 최소한의 얼리어답터의 개수를 구해야 한다.
A가 얼리어답터가 되기 위해서는, A의 친구들이 모두 얼리어답터여야 합니다.
즉 A와 연결된 모든 정점들이 얼리어답터여야합니다.
기본적인 DFS는 리프노드까지 진행한 후 과정을 진행하기에, 리프노드에서부터의 작업을 진행해야 합니다.
우선 저의 처음 접근방식은
내가 리프노드이고, 만약 부모가 얼리어답터가 아니라면, 그 부모를 얼리어답터로 만들어줬습니다.

1번->2번->4번->7번을 방문하고, 7번이 리프노드이기에, 7번과 연결된 4번을 얼리어답터로 만들어줬습니다.
8번과 9번은 4번이 얼리어답터이면, 자신들도 얼리어답터의 조건을 충족하기에, 상관없습니다.
이런 식으로 리프노드를 타고 올라가서, 부모노드를 얼리어답터로 바꿔주는 작업을 했습니다.
이러한 방법이 결과적으로 얼리어답터의 숫자를 최소한으로 사용할 거라고 생각했습니다.
하지만 멸망했습니다..
조건이 너무 단순했던 걸까요..? 아니면 최소한의 얼리어답터의 수를 못 구했던 걸까요..
그래서 풀이방식을 수정했습니다.
질문게시판을 보니 대부분 DP를 섞어서 풀었더라고요. DP.. 생각도 못했습니다. ㅠㅠ
우선 DP 방식의 기본적인 접근방법은 다음과 같습니다.
DP [idx][0] : idx가 얼리어답터일 때, 해당 노드 + 자식 노드 중 만족하는 최소한의 얼리어답터의 수입니다.
DP [idx][1] : idx가 얼리어답터가 아닐 때, 해당 노드 + 자식 노드 중 만족하는 최소한의 얼리어답터 수입니다.
이러한 작업도 리프노드에서 부터 거꾸로 올라가기 때문에, 잘 생각해봐야 합니다.

💡그림 설명
- DP [7][0] =1, DP [7][1]=0입니다.
- 8,9도 동일합니다.
- DP [4][0]=1, DP [4][1]=3입니다.
- 4가 얼리어답터라면, 7,8,9는 얼리어답터일 필요성이 없기 때문에, DP [4][0]는 1이고,
- 4가 얼리어답터가 아닐 경우, 7,8,9 모두 얼리어답터여야 하기 때문에, DP [4][1]=3입니다.
- 이런 식으로 쭉쭉 진행하다가, 우리가 필요한 것은 DP [1][0]과 DP [1][1] 두 값 중 최솟값입니다.
- 계속해서 아래에서 더해준 값을 DP로 저장하는 메모이제이션 방법을 사용합니다.
💻전체 코드
#include <iostream> #include <vector> #include <algorithm> #include <math.h> using namespace std; int n; int answer = 0; bool V[1000001]; vector<vector<int> >dp; vector<int> graph[1000001]; void funct(int idx); int main() { cin >> n; // n은 정점의 개수 int s, e; dp.resize(n+1,vector<int>(2,0)); for (int i = 0; i < n - 1; i++) { cin >> s >> e; graph[s].push_back(e); // s->e graph[e].push_back(s); // e->s } funct(1); answer=min(dp[1][0],dp[1][1]); cout<<answer<<endl; } void funct(int idx){ V[idx]=true; //방문처리. dp[idx][0]=1; // for(int i=0; i<graph[idx].size();i++){ int next=graph[idx][i]; //다음 방문할 지역 if(V[next]) //방문한 지역이라면 continue; funct(next); dp[idx][0]+=min(dp[next][0], dp[next][1]); //idx가 얼리어답터일때 dp[idx][1]+=dp[next][0]; //idx가 얼리어답터가 아닐때 } }
😀느낀 점
- 코드적으로는 굉장히 간단합니다.
- 접근방식이 트리 -> DP로 넘어가는 게 어려워서 골드 3이라는 난이도인 거 같습니다.
- 조건만 잘 이해한다면 그렇게 어려운 문제는 아니었습니다!
'CodingTest > Baekjoon' 카테고리의 다른 글
| [백준 14502] - 연구소(Kotlin)[골드4] (0) | 2023.08.10 |
|---|---|
| [백준 11967] - 불 켜기(C++)[골드2] (2) | 2023.07.05 |
| [백준 1967] - 트리의 지름(C++)[골드4] (1) | 2023.05.12 |
| [백준 9489] - 사촌(C++)[골드4] (1) | 2023.05.11 |
| [백준 21608] - 상어 초등학교(C++)[골드5] (0) | 2023.05.11 |
