문제
우주비행이 꿈이었던 진우는 음식점 '매일매일 싱싱'에서 열심히 일한 결과 달 여행에 필요한 자금을 모두 마련하였다! 지구와 우주사이는 N X M 행렬로 나타낼 수 있으며 각 원소의 값은 우주선이 그 공간을 지날 때 소모되는 연료의 양이다.
[예시]

진우는 여행경비를 아끼기 위해 조금 특이한 우주선을 선택하였다. 진우가 선택한 우주선의 특징은 아래와 같다.
1. 지구 -> 달로 가는 경우 우주선이 움직일 수 있는 방향은 아래와 같다.
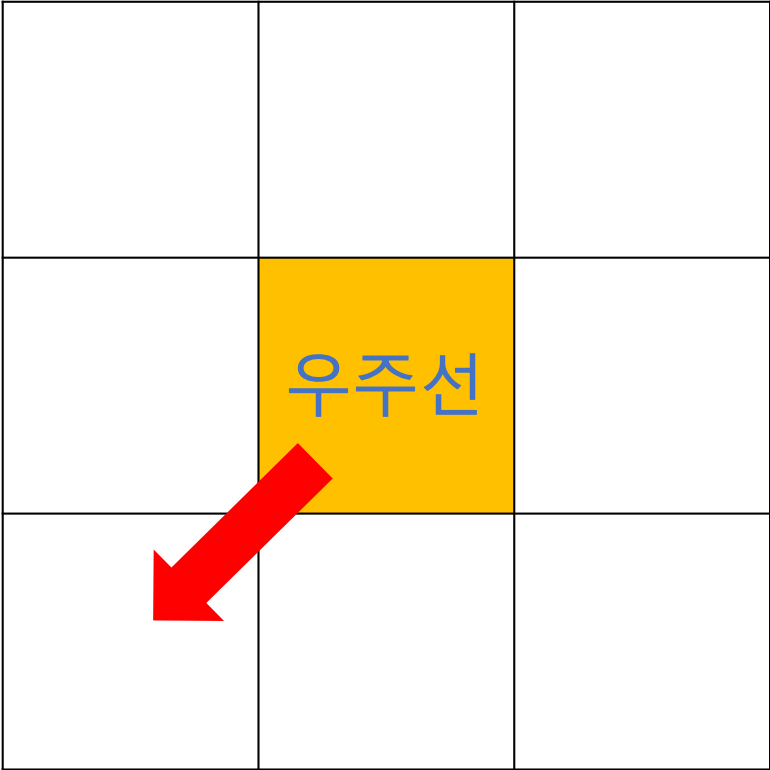

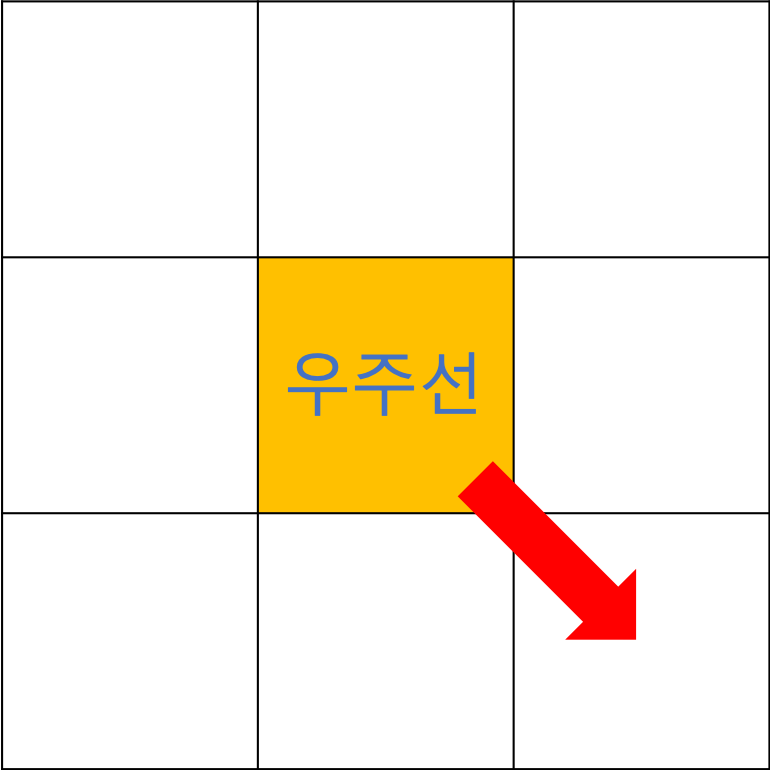
2. 우주선은 전에 움직인 방향으로 움직일 수 없다. 즉, 같은 방향으로 두 번 연속으로 움직일 수 없다.
진우의 목표는 연료를 최대한 아끼며 지구의 어느위치에서든 출발하여 달의 어느 위치든 착륙하는 것이다.
최대한 돈을 아끼고 살아서 달에 도착하고 싶은 진우를 위해 달에 도달하기 위해 필요한 연료의 최솟값을 계산해 주자.
입력
첫줄에 지구와 달 사이 공간을 나타내는 행렬의 크기를 나타내는 N, M (2 ≤ N, M ≤ 1000)이 주어진다.
다음 N 줄 동안 각 행렬의 원소 값이 주어진다. 각 행렬의 원소값은 100 이하의 자연수이다.
출력
달 여행에 필요한 최소 연료의 값을 출력한다.
문제 풀이
초기 풀이
초기 풀이는 DP 배열을 2차원 배열로 선언했다.
그리고 방향 배열도 2차원 배열로 선언해서 그 좌표에 대한 방향을 기록해 줬다.
진행하면서 이동할 수 있는 경로에 대해서 그 순간순간 최솟값을 찾아서 그때의 방향을 기록해 줬다.
이러니까 바로 틀렸다. 나는 그냥 그 현재지점과 이동하려는 길만 생각해 줬기 때문에 당연히 특정 테스트케이스에서
틀릴 수밖에 없었다..
나는 3차원 배열로 풀기 싫어서 2차원 배열을 2개 만들어서 풀었는데, 틀렸던 모양이다.
수정된 풀이
따라서 3차원 배열을 통해 X, Y, Dir를 모두 저장하는 배열을 생성해서 풀었다.
방향은 3개가 있으므로, 배열의 크기는 DP [N][M][3]이 될 것이다
- 3개의 방향으로 이동할 수 있다.
- 0 : ↙️ , 1 : ⬇️, 2 : ↘️
- 즉 화살표 방향으로 온다는 뜻이다.
- 3개의 경우의 수로 방향을 특정할 수 있다.
- 왼쪽 끝일 경우는 왼쪽 위(2) 방향에서 오는 경우가 없다.
- 따라서 방향은 0과 1만 신경 써주면 된다.
- 오른쪽 끝일 경우는 오른쪽 위(0) 방향에서 오는 경우가 없다.
- 따라서 방향은 1과 2만 신경 써주면 된다.
- 그 밖의 경우는 세 방향 모두 신경 써줘야 한다.
- 왼쪽 끝일 경우는 왼쪽 위(2) 방향에서 오는 경우가 없다.
쉽게 설명하자면,
DP [i][j][0] = 좌표(i,j)까지 가는데 ↙️이동을 한다는 뜻입니다.
따라서 DP[i][j][0] = DP [i-1][j+1][1]과 DP [i-1][j+1][2]의 최솟값을 더해줘야 합니다.
DP [i-1][j+1][0]을 포함시키지 않는 이유는 똑같은 방향으로 연속 이동이 불가능하기 때문입니다.
예를 하나 더 들자면,
DP [i][j][1] = 좌표 (i, j)까지 가는데 ⬇️ 이동을 한다는 뜻입니다.
따라서 DP [i][j][1]= DP [i-1][j][0]과 DP [i-1][j][2]의 최솟값을 더해줘야 합니다.
위에 설명과 동일하게 똑같은 방향으로 연속 이동이 불가능하기에 DP [i-1][j][1]은 제외시켜 줍니다.
위치에 따라서 방향을 제외시켜 주면서 최솟값을 비교해서 쭉쭉 더해주면 됩니다.
코드
#include <iostream>
#include <vector>
#include <algorithm>
#include <limits.h>
using namespace std;
int n, m;
vector<vector<vector<int> > >dp;
vector<vector<int> > graph;
void funct();
int main()
{
cin >> n >> m;
graph.resize(n, vector<int>(m, 0));
dp.resize(n,vector<vector<int> >(m,vector<int>(3,0)));
for (int i = 0; i < n; i++)
{
for (int j = 0; j < m; j++)
{
cin >> graph[i][j];
for(int k=0; k<3; k++){
dp[i][j][k]=graph[i][j];
}
}
}
funct();
int answer= INT_MAX;
for(int i=0; i<m; i++){ //도착지점에서 최소값을 찾아줌.
for(int j=0; j<3; j++){
if(answer>dp[n-1][i][j]){
answer=dp[n-1][i][j];
}
}
}
cout<<answer<<endl;
}
void funct(){
for(int i=0; i<n; i++){
for(int j=0; j<m;j++){
if(i==0){
for(int k=0; k<3; k++){ //초기 시작점들은 그냥 넣어줌.
dp[i][j][k]=graph[i][j];
}
continue;
}
//왼쪽 끝단 오른쪽 위에서 오는 방향은 존재하지 않기에 최대값을 넣어줌.
if(j==0){
dp[i][j][0]= graph[i][j]+min(dp[i-1][j+1][1],dp[i-1][j+1][2]);
dp[i][j][1]= graph[i][j]+min(dp[i-1][j][0],dp[i-1][j][2]);
dp[i][j][2]=INT_MAX;
}
else if(j==m-1){ //오른쪽 끝단 왼쪽 위에서 오는 경우는 존재하지 않기에 최대값을 넣어줌.
dp[i][j][1]= graph[i][j]+min(dp[i-1][j][0],dp[i-1][j][2]);
dp[i][j][2]= graph[i][j]+min(dp[i-1][j-1][0],dp[i-1][j-1][1]);
dp[i][j][0]=INT_MAX;
}
else{
dp[i][j][0] = graph[i][j]+min(dp[i-1][j+1][1],dp[i-1][j+1][2]);
dp[i][j][1] = graph[i][j] + min(dp[i-1][j][0],dp[i-1][j][2]);
dp[i][j][2]=graph[i][j]+min(dp[i-1][j-1][0],dp[i-1][j-1][1]);
}
}
}
}😀느낀 점
3차원 배열로 푸는 풀이를 그다지 선호하지 않았다. 왜냐하면 메모리 제한 때문이다.
하지만 배열의 최대 크기를 보고 메모리를 계산하는 방법을 몰라서 그랬던 거 같다.
앞으로는 배열의 최대 크기를 보고 메모리를 계산해서 효과적인 자료구조를 정해서 알고리즘을 풀어야겠다고 느꼈다.
'CodingTest > Baekjoon' 카테고리의 다른 글
| [백준 2011] - 암호코드(C++)[골드5] (0) | 2023.03.28 |
|---|---|
| [백준 7579] - 앱(C++)[골드3] (0) | 2023.03.25 |
| [백준 2580] - 스도쿠(C++)[골드4] (0) | 2023.03.18 |
| [백준 2138]- 전구와 스위치(C++)[골드5] (0) | 2023.03.17 |
| [백준 2529] - 부등호(C++)[실버1] (0) | 2023.03.15 |
