다익스트라 알고리즘은 그래프에서 한 정점(노드)에서 다른 정점까지의 최단 경로를 구하는 알고리즘이다.
[여기서 그래프에는 음의 가중치가 없어야 한다!]
왜냐하면 다익스트라 알고리즘은 탐욕 법(Greedy)을 기반의 알고리즘인데 최소 거리에 최소 거리를 계속 붙여가면서 최종적으로 최적의 경로를 찾기 때문에 음수 가중치를 고려하지 못하는 것이 현실이다.
하지만 무조건적으로 다익스트라 알고리즘이 음수 가중치가 포함된 그래프에서 최단경로를 못 구하는 것은 아니다.
구할 수도 있고, 못 구할 수도 있다.
자세한 것은 밑에 주소에 적혀 있고, 나도 이 블로그를 보면서 참고했다
https://kangworld.tistory.com/76https://kangworld.tistory.com/76
[Algorithm] 다익스트라 알고리즘 : 음수 간선이 있으면 안 되는 이유
인트로 [2021.11.15 오타 수정] 다익스트라 알고리즘은 가중치 그래프에서 최단 경로를 찾는 알고리즘이다. 단 가중치가 모두 양수라는 조건이 있다. 이러한 이유는 다익스트라 알고리즘은 그리디(
kangworld.tistory.com
만약 음수의 가중치를 고려하고싶다면 벨만-포드 알고리즘을 사용하면 최단 경로를 구할 수 있다.
⚡알고리즘의 동작 단계
해당 그래프가 있고 나는 V1에서 V2로 가는 최단 경로를 찾고 싶다.
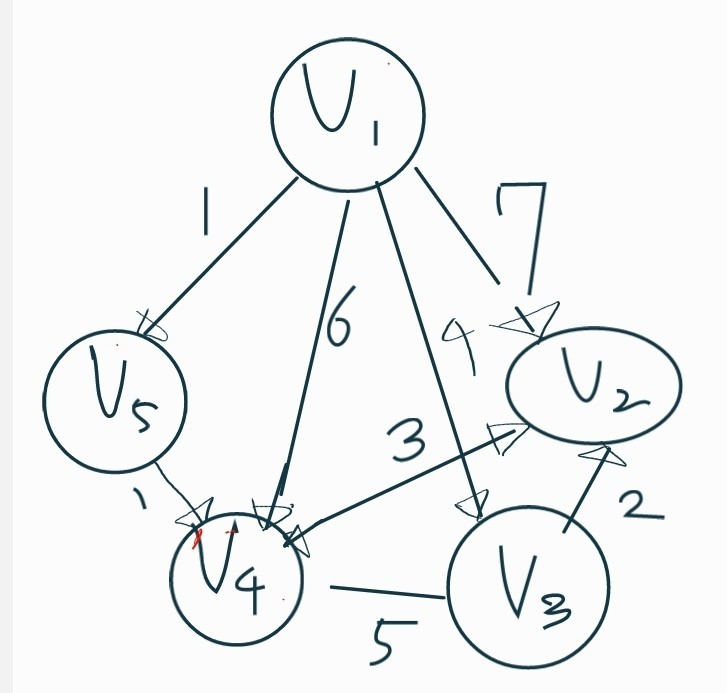
1. 우선 출발점을 V1으로 잡고, v1에서 갈 수 있는 모든 노드들까지의 거리를 계산한다.
| 0 | 7 | 무한 | 6 | 1 |
2.v5를 선택한다. 그 이유는 v1에서 갈 수 있는 노드들 중에서 가장 가까운 노드 이기 때문이다.

3.v5를 밟았으므로 거리테이블을 최신화해줌.
| 4. 인접 노드 중에서 |
방문하지 않고, 거리가 가까운 노드인 V4를 방문한다.
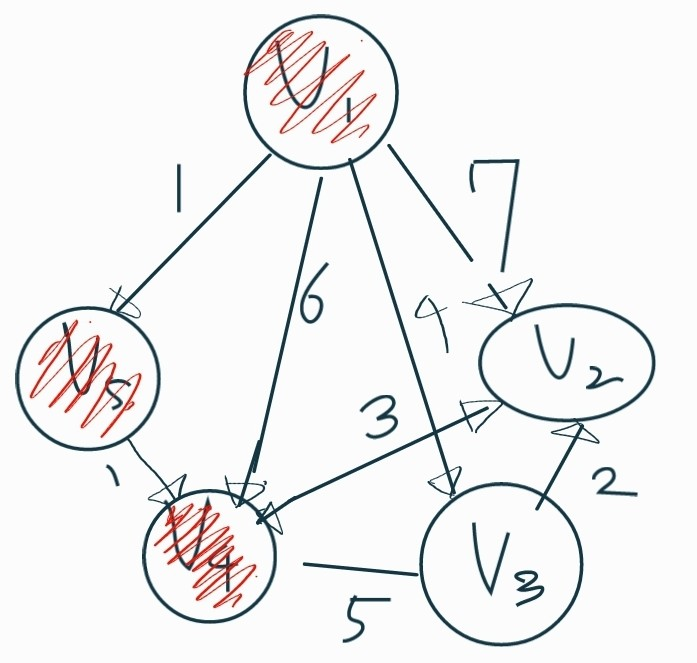
5.V4를 밟았기 때문에 거리테이블을 최신화해줌.
| 0(선택) | 7->5 | 4 | 2(선택) | 1(선택) |
6. 인접 노드 중 방문하지 않고 가장 작은 거리인 V3를 방문함.
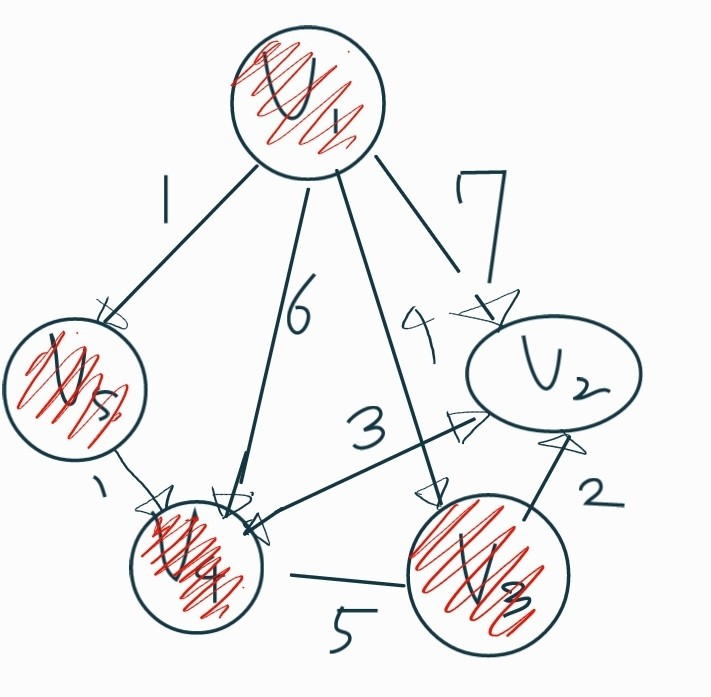
7.V3를 방문했으므로 거리 테이블을 최신화한다.
| 0(선택) | 5(선택) | 4(선택) | 2 | 1(선택) |
8. 이제 방문하지 않고 인접한 노드인 V2를 방문하고 탐색을 끝낸다.
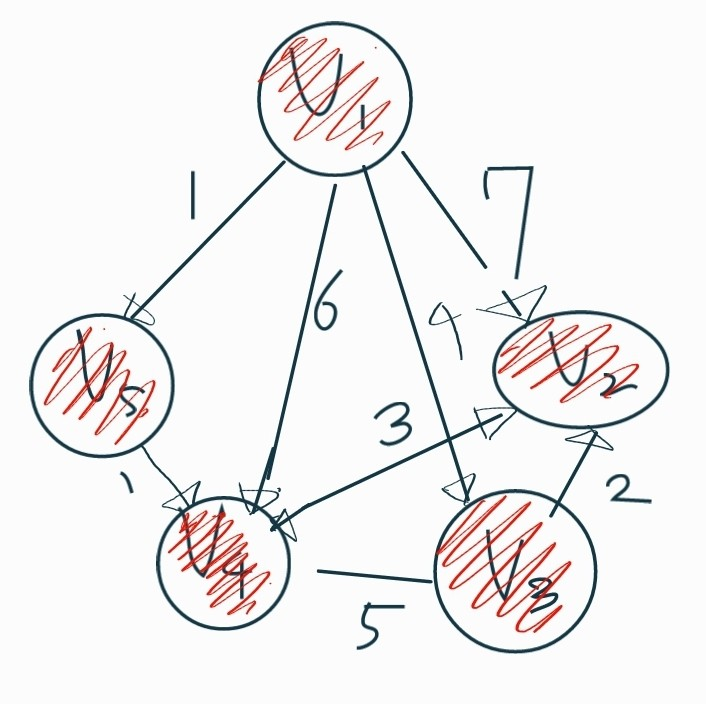
/*
directed graph
v1을 첫시작으로 뽑음.v1에서 가장 가까운 vertex를 선정해서 Y집합에 넣음.
Y집합(v1, v2) V- Y(v3, v4, v5) 그 다음 Y집합에서 가까운 것과 V - Y가까운것 대신 Y집합 노드를경유하는 결과값으로 해야함.
prim알고리즘과 dijkstra알고리즘은 비슷하다.차이는 nearest, distance 배열을 쓰는 prim이지만
dijkstra는 touch배열과 length배열을 사용한다.
touch배열은 v[i]->v1로 가는데 가까운 노드
length배열은 y집합에서 vi 까지 최소비용 경로
*/
#define INF 999999
#include <iostream>
#include <vector>
using namespace std;
typedef vector<vector<int>> matrix;
void dijkstra(int n, matrix& t, vector<pair<int, int>>& F);
int find(vector<int>& v, int n);
int n, m;
vector<int> touch(n + 1), length(n + 1);
int main()
{
cin >> n >> m;
touch.resize(n + 1, 0);
length.resize(n + 1, 0);
matrix a(n + 1, vector<int>(n + 1, INF));
vector<pair<int, int>> b;
vector<int> weight;
for (int i = 0; i < m; i++)
{
int s, f, w;
cin >> s >> f >> w;
a[s][f] = w;
}
dijkstra(n, a, b);
for (int i = 0; i < b.size(); i++)
{
int u = b[i].first, v = b[i].second;
cout << u << " " << v << " " << a[u][v] << endl;
}
int number, aa;
cin >> number;
for (int i = 0; i < number; i++)
{
// touch값이 1이 될때까지 넘김
cin >> aa;
vector<int> bb;
while (aa != 1)
{
bb.push_back(aa);
aa = touch[aa];
}
bb.push_back(1);
for (int i = bb.size() - 1; i >= 0; i--)
{
if (i > 0)
cout << bb[i] << " ";
else
cout << bb[i];
}
cout << endl;
}
}
void dijkstra(int n, matrix& t, vector<pair<int, int>>& F)
{
int vnear, min;
F.clear();
for (int i = 2; i <= n; i++) // v1을 고정시작점으로 하기 때문이다.
{
touch[i] = 1;
length[i] = t[1][i];
}
for (int i = 2; i <= n; i++)
{
if (i < n)
cout << touch[i] << " ";
else
cout << touch[i];
}
cout << endl;
for (int i = 0; i < n - 1; i++)
{
min = INF;
for (int i = 2; i <= n; i++)
{
if (0 <= length[i] && length[i] < min)
{
min = length[i];
vnear = i;
}
}
F.push_back(make_pair(touch[vnear], vnear)); //간선을 f에 넣어주기
// find(touch, vnear);
for (int i = 2; i <= n; i++)
{
if (length[i] > length[vnear] + t[vnear][i]) //기존 y조합에서의 dintance와 추가된 v간의 거리 계산
{
length[i] = length[vnear] + t[vnear][i];
touch[i] = vnear;
}
}
for (int i = 2; i <= n; i++)
{
if (i < n)
cout << touch[i] << " ";
else
cout << touch[i];
}
cout << endl;
length[vnear] = -1;
// num++;
}
}'Skils > Algorithm' 카테고리의 다른 글
| [알고리즘] - 누적합(1차원, 2차원) (0) | 2025.01.16 |
|---|---|
| 투 포인터 알고리즘(Two Pointer) (0) | 2023.03.29 |
| [알고리즘] DFS & BFS (0) | 2022.07.30 |
| [알고리즘 기말 이론] (0) | 2022.06.15 |
| [알고리즘] Intractability & NP-Theory (0) | 2022.06.13 |
다익스트라 알고리즘은 그래프에서 한 정점(노드)에서 다른 정점까지의 최단 경로를 구하는 알고리즘이다.
[여기서 그래프에는 음의 가중치가 없어야 한다!]
왜냐하면 다익스트라 알고리즘은 탐욕 법(Greedy)을 기반의 알고리즘인데 최소 거리에 최소 거리를 계속 붙여가면서 최종적으로 최적의 경로를 찾기 때문에 음수 가중치를 고려하지 못하는 것이 현실이다.
하지만 무조건적으로 다익스트라 알고리즘이 음수 가중치가 포함된 그래프에서 최단경로를 못 구하는 것은 아니다.
구할 수도 있고, 못 구할 수도 있다.
자세한 것은 밑에 주소에 적혀 있고, 나도 이 블로그를 보면서 참고했다
https://kangworld.tistory.com/76https://kangworld.tistory.com/76
[Algorithm] 다익스트라 알고리즘 : 음수 간선이 있으면 안 되는 이유
인트로 [2021.11.15 오타 수정] 다익스트라 알고리즘은 가중치 그래프에서 최단 경로를 찾는 알고리즘이다. 단 가중치가 모두 양수라는 조건이 있다. 이러한 이유는 다익스트라 알고리즘은 그리디(
kangworld.tistory.com
만약 음수의 가중치를 고려하고싶다면 벨만-포드 알고리즘을 사용하면 최단 경로를 구할 수 있다.
⚡알고리즘의 동작 단계
해당 그래프가 있고 나는 V1에서 V2로 가는 최단 경로를 찾고 싶다.

1. 우선 출발점을 V1으로 잡고, v1에서 갈 수 있는 모든 노드들까지의 거리를 계산한다.
| 0 | 7 | 무한 | 6 | 1 |
2.v5를 선택한다. 그 이유는 v1에서 갈 수 있는 노드들 중에서 가장 가까운 노드 이기 때문이다.

3.v5를 밟았으므로 거리테이블을 최신화해줌.
| 4. 인접 노드 중에서 |
방문하지 않고, 거리가 가까운 노드인 V4를 방문한다.

5.V4를 밟았기 때문에 거리테이블을 최신화해줌.
| 0(선택) | 7->5 | 4 | 2(선택) | 1(선택) |
6. 인접 노드 중 방문하지 않고 가장 작은 거리인 V3를 방문함.

7.V3를 방문했으므로 거리 테이블을 최신화한다.
| 0(선택) | 5(선택) | 4(선택) | 2 | 1(선택) |
8. 이제 방문하지 않고 인접한 노드인 V2를 방문하고 탐색을 끝낸다.

/* directed graph v1을 첫시작으로 뽑음.v1에서 가장 가까운 vertex를 선정해서 Y집합에 넣음. Y집합(v1, v2) V- Y(v3, v4, v5) 그 다음 Y집합에서 가까운 것과 V - Y가까운것 대신 Y집합 노드를경유하는 결과값으로 해야함. prim알고리즘과 dijkstra알고리즘은 비슷하다.차이는 nearest, distance 배열을 쓰는 prim이지만 dijkstra는 touch배열과 length배열을 사용한다. touch배열은 v[i]->v1로 가는데 가까운 노드 length배열은 y집합에서 vi 까지 최소비용 경로 */ #define INF 999999 #include <iostream> #include <vector> using namespace std; typedef vector<vector<int>> matrix; void dijkstra(int n, matrix& t, vector<pair<int, int>>& F); int find(vector<int>& v, int n); int n, m; vector<int> touch(n + 1), length(n + 1); int main() { cin >> n >> m; touch.resize(n + 1, 0); length.resize(n + 1, 0); matrix a(n + 1, vector<int>(n + 1, INF)); vector<pair<int, int>> b; vector<int> weight; for (int i = 0; i < m; i++) { int s, f, w; cin >> s >> f >> w; a[s][f] = w; } dijkstra(n, a, b); for (int i = 0; i < b.size(); i++) { int u = b[i].first, v = b[i].second; cout << u << " " << v << " " << a[u][v] << endl; } int number, aa; cin >> number; for (int i = 0; i < number; i++) { // touch값이 1이 될때까지 넘김 cin >> aa; vector<int> bb; while (aa != 1) { bb.push_back(aa); aa = touch[aa]; } bb.push_back(1); for (int i = bb.size() - 1; i >= 0; i--) { if (i > 0) cout << bb[i] << " "; else cout << bb[i]; } cout << endl; } } void dijkstra(int n, matrix& t, vector<pair<int, int>>& F) { int vnear, min; F.clear(); for (int i = 2; i <= n; i++) // v1을 고정시작점으로 하기 때문이다. { touch[i] = 1; length[i] = t[1][i]; } for (int i = 2; i <= n; i++) { if (i < n) cout << touch[i] << " "; else cout << touch[i]; } cout << endl; for (int i = 0; i < n - 1; i++) { min = INF; for (int i = 2; i <= n; i++) { if (0 <= length[i] && length[i] < min) { min = length[i]; vnear = i; } } F.push_back(make_pair(touch[vnear], vnear)); //간선을 f에 넣어주기 // find(touch, vnear); for (int i = 2; i <= n; i++) { if (length[i] > length[vnear] + t[vnear][i]) //기존 y조합에서의 dintance와 추가된 v간의 거리 계산 { length[i] = length[vnear] + t[vnear][i]; touch[i] = vnear; } } for (int i = 2; i <= n; i++) { if (i < n) cout << touch[i] << " "; else cout << touch[i]; } cout << endl; length[vnear] = -1; // num++; } }
'Skils > Algorithm' 카테고리의 다른 글
| [알고리즘] - 누적합(1차원, 2차원) (0) | 2025.01.16 |
|---|---|
| 투 포인터 알고리즘(Two Pointer) (0) | 2023.03.29 |
| [알고리즘] DFS & BFS (0) | 2022.07.30 |
| [알고리즘 기말 이론] (0) | 2022.06.15 |
| [알고리즘] Intractability & NP-Theory (0) | 2022.06.13 |
