[알고리즘] - 누적합(1차원, 2차원)
누적합이란?
누적합(Prefix Sum)은 배열이나 리스트에서 특정 구간의 합을 빠르게 계산하기 위해 사용하는 알고리즘 기법입니다.
일반적으로 입력 배열의 첫 번째 원소부터 특정 위치까지의 합을 저장한 배열을 말하며, 사용됩니다.
즉, 배열의 원소들을 더한 중간 결과를 미리 저장함으로써, 반복 계산을 최소화하고 효율성을 높입니다.
예시 그림을 살펴보면 이해가 쉬울 것입니다.

입력으로 [2,4,6,8,10] 이라는 배열이 주어진다면, 누적합은 위와 같이 구할 수 있습니다.
그렇다면 왜 누적합을 사용해야 할까요?
누적합을 사용하는 이유
효율적인 구간 합 계산
일반적으로 배열에서 특정 구간의 합을 구하려면, 해당 구간의 원소를 하나씩 더해야 합니다.
이 경우 시간복잡도는 구간의 길이인 O(n)이 됩니다.
하지만 누적합 배열을 사용하면 구간의 합을 O(1)로 구할 수 있습니다.
누적합은 특정 위치까지의 합을 저장하기 때문에 누적합의 성질을 이용하면 쉽게 구할 수 있습니다.

예를 들어 우리가 2번째~4번째의 구간 합을 알고 싶다면 두 가지 접근 방법으로 구할 수 있습니다.
첫 번째로, 누적합 배열만을 이용해서 구할 수 있습니다.
A [4](4번까지의 합 정보가 저장됨) - A [1](1번까지의 합 정보가 저장됨)을 연산하면 2~4번까지의 구간합이 구해집니다.
두 번째로, 누적합 배열과 원본 숫자 배열을 이용해서 구할 수 있습니다.
A [4](4번까지의 합 정보가 저장됨) - A [2](2번까지의 합 정보가 저장됨) + N [2](2번 숫자)을 연산하면 구간합이 구해집니다.
중복 계산 방지
배열에서 여러 번 구간 합을 계산해야 하는 경우, 매번 원소를 하나씩 더하면 중복 계산이 발생하기 마련입니다.
누적합은 한 번의 전처리로 이러한 중복 계산을 방지할 수 있습니다.
꿀팁
보통의 누적합은 이전 누적합의 정보와 현재 숫자의 정보를 더해서 배열을 구현합니다.
하지만 배열의 시작은 0번 index이기 때문에, 이러한 연산 처리에 굉장히 까다롭습니다.
따라서, 배열의 시작지점을 0번이 아닌 1번으로 시작시켜서 연산 처리에 편리함을 더하는 테크닉도 있습니다.
코드
public static void main(String[] args) throws IOException {
br = new BufferedReader(new InputStreamReader(System.in));
st = new StringTokenizer(br.readLine());
n = Integer.parseInt(st.nextToken());
int[] num = new int[n + 1]; // 숫자 배열 1번 인덱스를 시작지점으로 하기 때문에 크기를 1 증가시킴
int[] sum = new int[n + 1]; // 누적합 배열
st = new StringTokenizer(br.readLine());
for (int i = 1; i <= n; i++) { // 배열의 시작 인덱스를 1로 변경
num[i] = Integer.parseInt(st.nextToken());
sum[i] = sum[i - 1] + num[i];
}
st = new StringTokenizer(br.readLine());
int start = Integer.parseInt(st.nextToken()); // 구하려는 누적합 시작 구간
int end = Integer.parseInt(st.nextToken()); // 구하려는 누적합 끝 구간
int answer1 = sum[end] - sum[start - 1];
int answer2 = sum[end] - sum[start] + num[start];
System.out.println(answer1 + " == " + answer2 + " " + (answer2 == answer1));
}
위에서는 1차원 누적합에 대해서 다뤘다면 지금부터는 2차원 누적합에 대해 다뤄보겠습니다.
2차원 누적합은 1차원 누적합보다 복잡하지만, 규칙을 발견하다면 쉽게 응용할 수 있습니다.

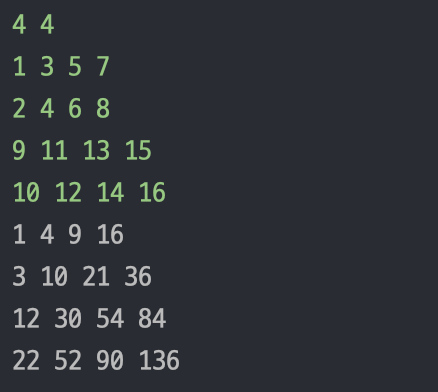
위와 같은 4*4 2차원 배열이 있다고 생각해 봅시다.
(2,2) ~ (4,4)까지의 합을 구하면 다음과 같습니다.
4+6+8+11+13+15+12+14+16 = 99가 됩니다.
손으로, 눈으로 하면 정말 쉽지만 코드적으로 풀어내려면 머리가 조금 띵해지실 것입니다.
그림을 그려보면서 구하면 조금 쉽게 접근할 수 있습니다.
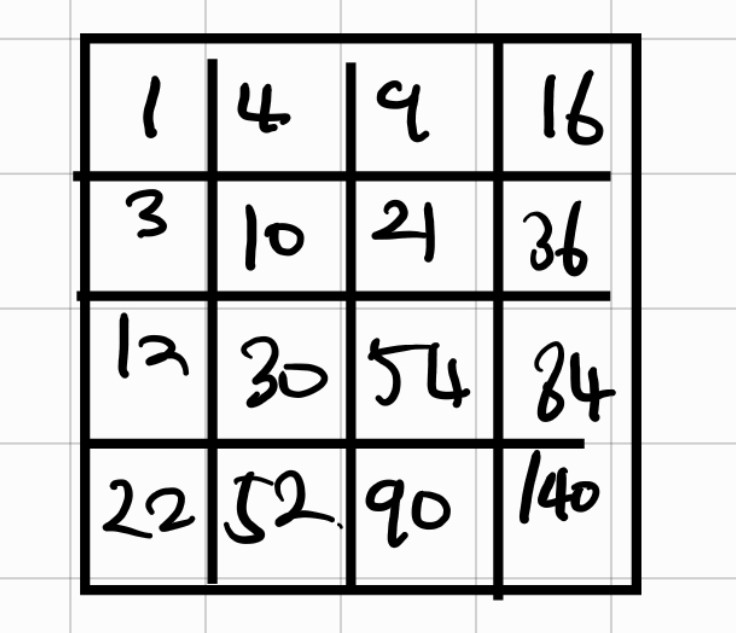
위 그림은 1x1부터 4x4까지의 이차원 누적합을 저장한 배열입니다.
여기서 (1,1) ~ (2,2)의 누적합을 구하는 과정을 예로 들어 설명하면 이해하기 쉬울 것입니다.
지금부터는 원본 배열을 건들지 않고, 누적합만을 이용해서 구해보도록 하겠습니다.
2,2의 누적합은 다음과 같이 구할 수 있습니다.

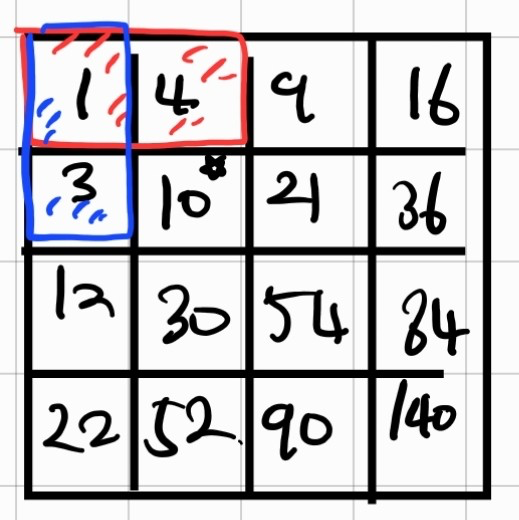
빨간 영역의 누적합과, 파란 영역의 누적합 그리고 4를 더한 값에 중복된 1을 빼주면 10이라는 결과가 나오게 됩니다.
즉 2차원의 누적합에선 중복이 발생할 수밖에 없습니다. 왜냐하면 왼쪽에서 접근하고, 위쪽에서 접근하는데 두 방향은 중복된 원소를 가질 수 밖에 없습니다.
이걸 식으로 바꿔볼까요?
S[2][2] = S[1][2]([1,1] ~ [1,2] 합이 저장됨) + S[2][1]([1,1] ~ [2,1] 합이 저장됨) + A[2][2](원래 숫자) - A[1][1](중복 숫자)
이제 영역을 확장해서 생각해 보겠습니다.
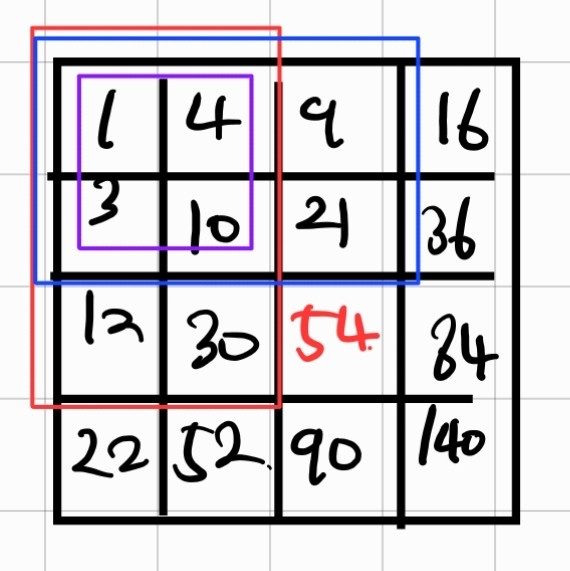
(1,1) ~ (3,3)의 구간합인 54를 구하기 위해서는 표시된 영역들과 (3,3) 위치에 있는 숫자가 필요합니다.
빨간색 영역과 파란색 영역을 더하는 과정에서 보라색의 영역이 중복이 발생하게 됩니다.
이 중복을 제거해 줘야 정확한 누적합을 구할 수 있습니다.
이제 우리가 원하는 (i, j)로 공식화해보겠습니다.
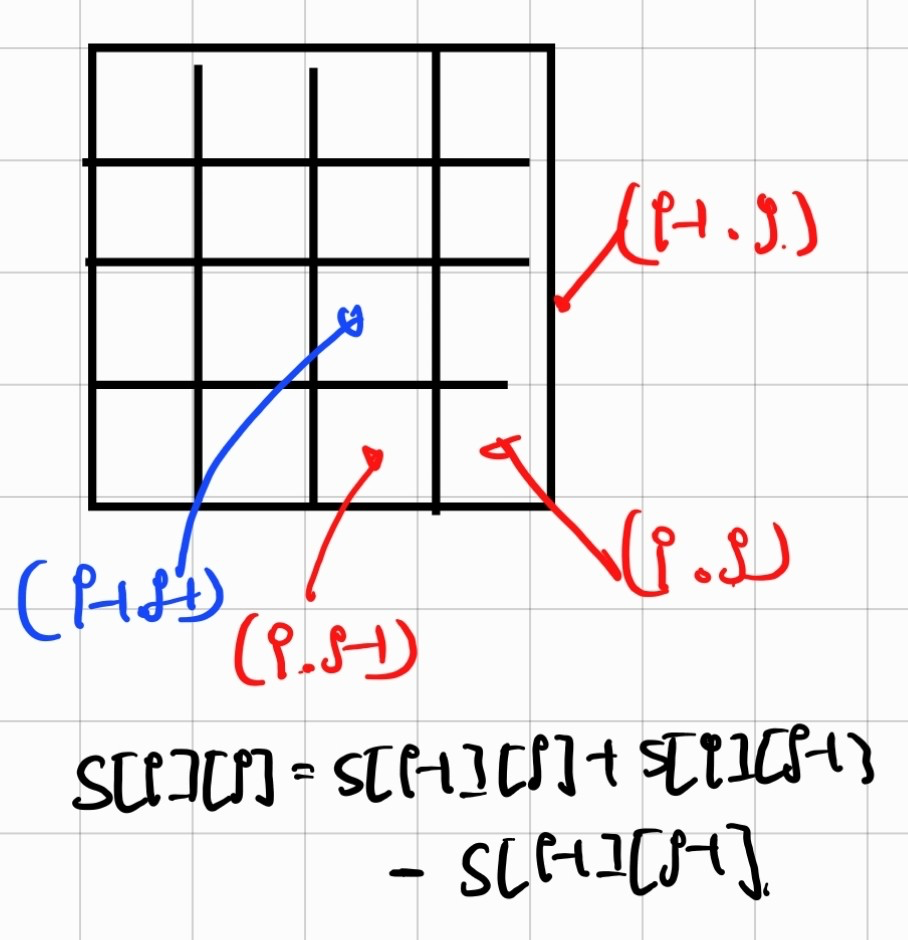
구현은 다음과 같습니다.
public static void main(String[] args) throws IOException {
br = new BufferedReader(new InputStreamReader(System.in));
st = new StringTokenizer(br.readLine());
n = Integer.parseInt(st.nextToken());
m = Integer.parseInt(st.nextToken());
int[][] num = new int[n + 1][m + 1];
int[][] sum = new int[n + 1][m + 1];
for (int i = 1; i <= n; i++) {
st = new StringTokenizer(br.readLine());
for (int j = 1; j <= m; j++) {
num[i][j] = Integer.parseInt(st.nextToken());
sum[i][j] = sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1] + num[i][j];
}
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
System.out.print(sum[i][j] + " ");
}
System.out.println();
}
}
꿀팁
특정 문제에서 특정 크기만큼 구간을 잘라서 구간합을 구하는 문제도 있습니다.
예를 들어 (2,2) ~ (4,4)를 구한다던지와 같은 문제가 있는데 그럴 경우는 다음과 같이 구현할 수 있습니다.
for (int i = k; i <= n; i++) {
for (int j = k; j <= m; j++) {
cnt = Math.min(
cnt,
sum[i][j] - (sum[i - k][j] + sum[i][j - k] - sum[i - k][j - k])
);
}
}
만약 좌표가 (4,4)이고 크기가 3인 사각형이라면 (2,2) ~ (4,4)의 구간합을 구하는 구현식입니다.
누적합은 간단한 아이디어지만, 전처리, 중복 계산 방지와 같은 효율성을 크게 개선할 수 있는 강력한 기법입니다.
1차원 누적합은 간단하고, 금방 떠올릴 수 있지만 2차원 누적합은 한번 풀어보고 익혀서 푸는 것이 코딩테스트나, 다른 응용에서 쉽게 떠올릴 수 있다고 생각합니다.
