[백준 2616] - 소형기관차(Kotlin)[골드3]
문제
https://www.acmicpc.net/problem/2616
2616번: 소형기관차
첫째 줄에 기관차가 끌고 가던 객차의 수가 입력된다. 그 수는 50,000 이하이다. 둘째 줄에는 기관차가 끌고 가던 객차에 타고 있는 손님의 수가 1번 객차부터 차례로 입력된다. 한 객차에 타고 있
www.acmicpc.net
문제 풀이
문제를 읽고 누적합을 구해서 소형차를 배정하는 문제인 것 같았다.
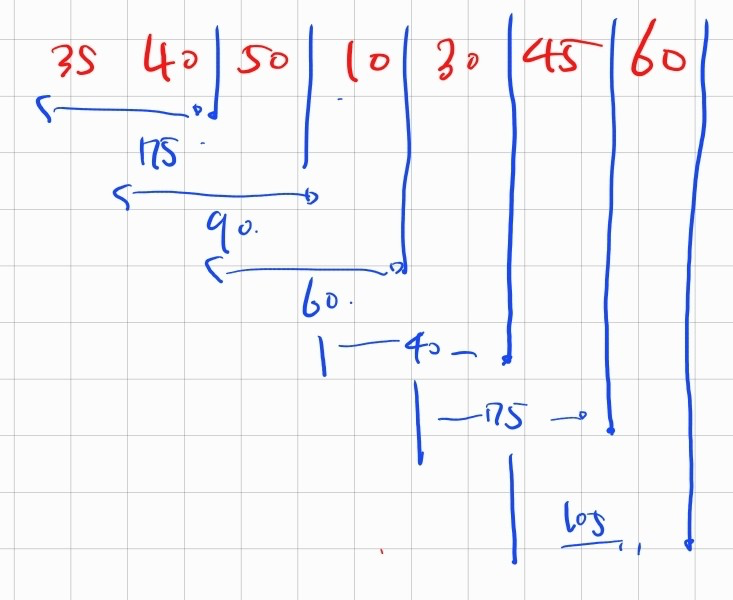
문제에서 주어진 테스트케이스에 대해서 먼저 누적합에 대한 그림을 그려보았다.
처음으로 접근한 방법은 정해진 구간까지의 최대 누적합을 구하는 방법으로 접근했다.
예를 들어 50까지 접근했을때의 최댓값은 40과 50을 태운 90이다.
다음으로 10까지 접근했을때의 최댓값은 40과 50을 태운 90 vs (35+40), (50+10)중 후자의 값이었다.
구간별로 배정할 수 있는 최대의 값을 구했다.
private fun getAccumulateSum() {
for (i in 0 until k) {
sum[k - 1] += ary[i]
}
for (i in k until n) {
sum[i] = sum[i - 1] - ary[i - k] + ary[i]
}
dp[k - 1] = sum[k - 1]
for (i in k until n) {
dp[i] = max(dp[i - 1], dp[i - k] + sum[i])
}
}
문제에서 주어진 테스트케이스에 대해선 정답이 나왔지만, 소형차가 3대라는 점과, 연속적으로 뽑지 않을 경우도 있기 때문에
특정테스트케이스에 대해서 통과하지 못했다.
따라서 소형차 3대에 대한 정보와 차를 배정했는지에 대한 여부를 판단해야 했기에, DP 배열을 2차원으로 접근하는 것이 맞다고 생각했다.
초기에 정의한 1차원 DP 배열은 다음과 같다.
dp[i] = index i까지 k개의 칸을 고려했을 때의 최대 누적합
수정한 2차원 DP 배열은 다음과 같다.
dp[i][j] = i번째 소형차를 j칸까지 검사했을 때의 최대 합
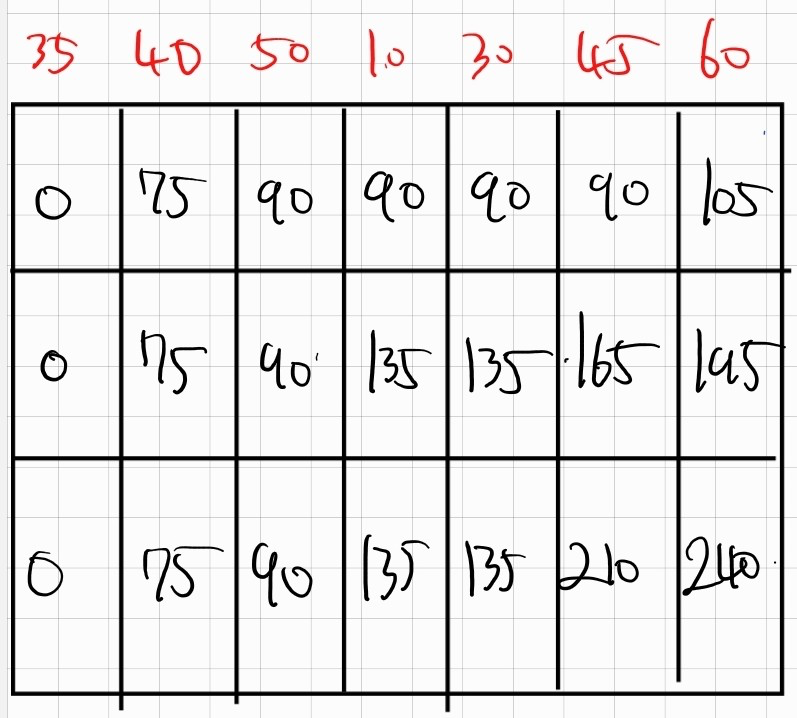
첫 번째 소형차에 대해서 최댓값은 (45,60)의 구간을 담는 105가 최댓값이다.
다음으로 두 번째 소형차의 구간은 첫번째 소형차의 정보를 이용해서 계산해야 한다.
두번째 소형차의 최댓값은 첫 번째에서 (40,50)을 담은 90과 (45,60)을 담은 105를 더한 195가 최대일 것이다.
다음으로 세 번째 소형차의 구간은 첫번째, 두번째 소형차의 정보를 이용해서 계산해야 한다.
세번째 소형차의 최댓값은 (35,40) + (50,10) + (45,60)인 240이 최댓값일 것이다.
어떻게 구할 수 있을까?
배낭 문제와 유사하게 접근하면 된다.
예를 들어 60을 마지막으로 소형차를 배정할 때, 2번째 소형차에서 60을 담지 않는 구간인 30까지의 최댓값을 이용해야 한다.
60을 담기 위해선 45,60을 이전 소형차가 배정받으면 안 된다.
즉 소형차의 배정칸 이전 구간을 확인하면 된다.
따라서 dp 점화식은 다음과 같다.
dp[i][j] = maxOf(dp[i-1][j], dp[i][j-1], dp[i-1][j-소형차칸] + j칸 까지의 누적합
dp[i-1][j]와 dp[i][j-1]이 추가된 이유는 해당 칸을 배정받지 않았을 때를 의미한다.
마지막 조건은 해당 칸을 배정받았을 때를 의미한다.
전체 코드
class Solution {
private val br = System.`in`.bufferedReader()
private var n = 0
private var k = 0
private lateinit var ary: IntArray
private lateinit var sum: IntArray
private lateinit var dp: Array<IntArray>
fun run() {
input()
getAccumulateSum()
solve()
print(dp[3][n])
}
private fun input() {
n = br.readLine().toInt()
ary = br.readLine().split(" ").map { it.toInt() }.toIntArray()
sum = IntArray(n + 1)
dp = Array(4) { IntArray(n + 1) }
k = br.readLine().toInt()
}
private fun solve() {
for (i in 1..3) {
for (j in k..n) {
dp[i][j] = maxOf(dp[i - 1][j], dp[i][j - 1], dp[i - 1][j - k] + sum[j - 1])
}
}
}
private fun getAccumulateSum() {
for (i in 0 until k) {
sum[k - 1] += ary[i]
}
for (i in k until n) {
sum[i] = sum[i - 1] - ary[i - k] + ary[i]
}
}
}
fun main() {
val solution = Solution().run()
}