Skils/Algorithm
[알고리즘-C++] 외판원 순회 문제(Dynamic Programming)
재한
2022. 5. 29. 13:36
문제 목표
n개의 도시로 판매 출장을 계획하고 있는 외판원이 각 도시를 한 번씩 방문하고, 다시 출발한 도시로 돌아오는 가장 짧은 여행길을 찾는 것.
--> 최단 경로 문제
--> 출발한 도시로 다시 돌아오는 부분에서 해밀턴 회로와 동일한 개념.
이 문제는 weighted, directed graph이다.
각 도시에서 도시로 가는 비용이 있고, 방향이 정해져 있다.(여기서 비용은 음이 아닌 정수로 가정한다)
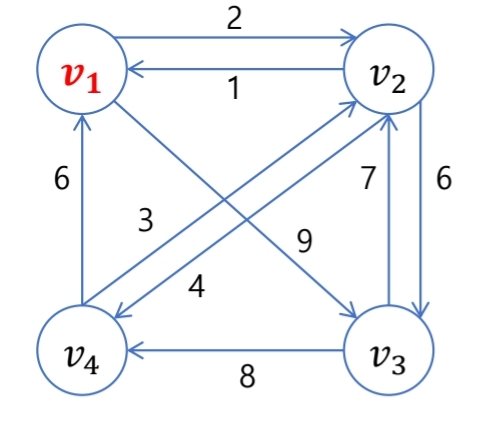
만약 v1을 출발점으로 잡는다면 가능한 경로와 그에 비용은 아래와 같다.
- [v1->v2->v3->v4->v1] = 22
- [v1->v3->v2->v4->v1] = 26
- [v1->v3->v4->v2->v1] = 21
v1에서 출발할때의 최적의 경로는 [v1->v3->v4->v2->v1]이고 그 비용은 21이다.
용어 정리
- V=모든 도시의 집합
- A=V의 부분 집합
- W=그래프의 인접행렬식. (경로가 없다면 ∞를 표현함, 자기 자신은 0)
- D [v][A] = A에 속한 도시를 각각 한번 씩만 거쳐서 v에서 출발점으로 가는 최단 경로의 길이
- A={v3}이고, D[2][A]의 값을 구한다면
- v2->v3->v1로 가는 경로가 D [2][A]가 될 것이다. 2->3->1로 가는 경로는 없기 때문에 D [2][A]는 ∞이다.
- A={v3, v4}이고, D [2][A]를 구한다면
- v2->v3->v4->v1 VS v2->v4->v3->v1중에서 최단 경로가 D [2][A]가 될 것이다.
- [v2->v3->v4->v1]=20 , [v2->v4->v3->v1]=∞이다.
- 따라서 D[2][A]는 더 작은 값인 20을 채택하게 된다.
- 20+ 출발점에서->v2로 가는 비용이 최솟값이면 이 경로가 최소값이 된다.
- v2->v3->v4->v1 VS v2->v4->v3->v1중에서 최단 경로가 D [2][A]가 될 것이다.
- 식을 세워보면 D [vi][A]=(W [i][j]+D [j][A-{vj}])중에서 최솟값이 될 것이다.
- 여기서 j는 A에 속하는 도시여야 한다.
- 그리고 A가 공집합이라면 D [vi][A]=W [i][1](vi에서 출발점까지 가는 경로)
- 최종적으로는 D [1][A]를 구하면 된다.(여기서 A는 V에서 v1을 빼고 모두를 포함하는 집합이 여야 한다.)
- A={v3}이고, D[2][A]의 값을 구한다면
A집합을 어떻게 구현해야 할지에 대해 많은 고민을 했다.
- 도시 개수만큼 vector를 만들고 지워준다?
- map의 도시를 넣고 방문하면 지워준다?
- 강의 자료를 참고하겠다. 엄청 편리하고 획기적인 방법인 것 같다.

- 비트 연산자를 이용하는 방법이다.
- 만약 A 집합이 {v2, v4}를 가지고 있다면 v2에 해당하는 001과 v4에 해당하는 100을 or연산해주면 된다.
- 이렇게 하면 편리한 점이 차집합을 계산할 때와 A에 해당 도시가 있는지 검사할 때 편리하다는 것이 장점이다.
구현
1. 배열 설명
D.resize(n + 1, vector<int>(pow(2, n - 1), 999)); // 0~4까지
W.resize(n + 1, vector<int>(n + 1, INF)); // 0~4까지
P.resize(n + 1, vector<int>(pow(2, n - 1), -1)); // 0~4까지 //0~7까지- D [v][A] = A에 속한 도시를 각각 한번 씩만 거쳐서 v에서 출발점으로 가는 최단 경로의 길이
- W=그래프의 인접 행렬식. (경로가 없다면 ∞를 표현함, 자기 자신은 0)
- P [i][j]는 i에서 j까지 갈 때 i 바로 뒤에 오는 도시를 의미함. 경로 : i -> P[i][j]
2.W배열 설정
for (int i = 0; i < m; i++)
{
int s, f, l;
cin >> s >> f >> l;
W[s][f] = l;
}
for (int i = 1; i <= n; i++)
{
W[i][i] = 0;
}- 입력받은 출발, 도착, 가중치를 입력해주고 인접 행렬이기 때문에 자기 자신으로 가는 지점은 0으로 초기화해줌.
3. D배열 초기 설정
for (i = 2; i <= n; i++)
{
D[i][0] = W[i][1]; //바로 가는 경로
}- D배열은 i에서 출발해서 j를 거쳐서 출발점으로 가는 경로지만 만약 j가 0이라면 i에서 출발점으로 바로 가는 경로를 넣어주면 된다.
4. 주요 함수 설명
- Count : A집합에서 도시가 몇 개 포함되어있는지 카운트하는 함수.
- 도시의 개수가 곧 A에서 1의 개수이다.
int Count(int A) //A집합에 도시가 몇개 있는지 카운트함. A집합에서 1의 개수가 도시의 개수를 뜻함.
{
int cnt = 0;
for (; A != 0; A >>= 1) // A>>1은 A를 한칸씩 오른쪽으로 옮겨줌.
{
if (A & 1)
cnt++;
}
return cnt;
}- IsIn : 지금 현재 내가 찍은 도시가 A집합에 있는지 확인하는 함수
- 만약 i가 A집합에 있다면 true를 return, i가 A집합에 없다면 false를 return
- 왜 1을 i-2만큼 왼쪽으로 이동시키는지에 대해서 설명하겠다.
- A집합 설계과정에서 v2를 001, v3를 010, v4를 100으로 잡았다. 여기서 i와 v2가 일치할려면 어떻게 해야할까?
- 1은 001이다. v2와 1을 대응할려면 1은 그대로여야한다. 따라서 1을 0칸, v3와 대응할려면 1을 왼쪽으로 1칸, v4와 대응할려면 1을 왼쪽으로 2칸 따라서 1을 i-2만큼 왼쪽으로 이동시켜줘야한다.
bool isIn(int i, int A)
//A집합에 i가 있는지 체크를 함. 있다면 true, 없다면 false를 리턴. v2부터 시작하므로 i-2자리만큼 왼쪽으로 이동시켜줘야함.
//예를 들어 2는 001, 3은 010, 4는 100 --> 001을 2는 0칸 3은 1칸 4는 2칸 왼쪽으로 이동시켜야 하므로 i-2만큼 왼쪽으로 이동시켜준다.
{
return (A & (1 << (i - 2))) != 0; // 1의 비트를 왼쪽으로 i-2만큼 이동시킴.
}- minimum : 최단 길이를 구해줌.
- value는 W[i][j](i에서 j를 거치고)+D[j][A](j에서 A집합에 있는 도시들을 거쳐서 i로 가는 길이)이다.
- 그렇다면 당연히 A집합에는 j가 포함되있어야함. IsIn을 통해서 j가 A에 있는지 체크후 없다면 continue, 있다면 코드를 진행한다.
- value값에서 도시를 하나씩 넣어주고, D[j][A]에서 j를 출발점으로 찍엇기때문에 A집합에서 j를 빼줘야한다.
int minimum(int n, int i, int &minJ, int A)
//최소경로 길이를 구하는 함수.
//나는 A집합에 있는 도시들중 하나를 선정해서 최소경로를 구하고싶다. 따라서 J가 A에 있어야한다.
{
int minV = INF, value;
for (int j = 2; j <= n; j++)
{
if (isIn(j, A)==0) //j가 A집합에 없다면 진행하면 안됨.
continue;
int value = W[i][j] + D[j][diff(A, j)];
if (minV > value)
{
minV = value;
minJ = j; //그떄의 최소값에 도시를 minj에 넣어줌.
}
}
return minV;
}- diff : 차집합 함수 -> A집합에서 도시를 방문했다면 그 도시는 빼고 또다시 경로를 짜야함.
- 만약 A가 111이라면 {v2,v3,v4}를 포함한다는 뜻이다. 그리고 j가 v3을 뜻하는 010이라면 어떻게 A에서 v3을 빼줘야할까?
- v3의 비트는 010이다. 1을 3-2만큼 왼쪽으로 이동시키면 010이 나온다.(IsIn에 자세한 설명이 있음.)
- 그렇다면 111에서 010을 빼야하는데 이 방법은 010을 not연산하면 101이 된다.
- 그러고 111과 101을 And 연산하면 101이 되므로 v3만 A집합에서 빠지게 된다!!.
int diff(int A, int j) //A집합에서 j에 해당하는 도시를 빼주는 함수.
//예를 들어 A가 111이고 j가 010이라면 j만 빼주는 방법은 j를 101(not계산)해서 A와 j를 and연산하면 된다.
{
return (A & ~(1 << (j - 2))); // 0과 1을 바꿈.
}- tour : 경로 구하는 함수
- P[i][j]는 i에서 j로 가는 경로중에서 i가 가장 빨리 밟는 도시이다.
- 출발점 v에서 최적의 경로는 v->k로 가고 A집합에서 k를 밟았으니 빼주고, 다시 k에서 또 P[k][A]를 구해서 진행하고 만약 A집합이 공집합이라면 마지막 도착지는 1이어야 하기때문에 1을 넣어준다.
void tour(int v, int A, vector<vector<int>> &P) //경로를 구하는 함수.
//P[i][j]는 i->j까지 가는 경로에서 i가 첫번째로 밟는 도시이다.
//그럼 내가 출발점에서 모든 도시를 거쳐서 가는 경로중에서 첫번째가 k에 들어가고
//그 k를 출발점으로 선정후 k를 방문했으니 A집합에서 k를 빼줌.
//위 과정 반복
//만약 A가 0이라면 모든 도시를 방문했다는 뜻이니까 출발점으로 되돌아가야하기때문에 경로에 1을 추가해줌.
{
int k = P[v][A];
if (A == 0) //맨마지막에 경로는 1이여야함.
path.push_back(1);
else
{
path.push_back(k);
tour(k, diff(A, k), P);
}
}- TSP 함수
- 부분집합의 개수를 구해야한다. 그 부분집합의 개수가 A집합의 최대개수이다.
- 2^(N-1)인 이유는 A집합에서는 출발점을 뺴줘야 하기 때문이다.
void travel(int n, vector<vector<int>> &P, int &minlength)
{
int A, j, i; // A의 집합을 표현할려면 2진수 개념을 사용
//부분집합의 개수는 2^N-1개이다. N-1인 이유는 v1은 집합에 포함 안하기때문이다.
int Size = pow(2, n - 1);
for (i = 2; i <= n; i++)
{
D[i][0] = W[i][1]; //바로 가는 경로
if (D[i][0] != INF)
Cnt++;
}
for (int k = 1; k <= n - 2; k++)
// k는 내가 방문하고자 하는 도시의 개수. 총 n-2개의 도시를 방문해서 구하고 마지막 도시는 나중에 추가해줌.
//만약 n-1개를 방문했다면 그건 종결을 뜻함. n-2개 구하고 A집합에서 남은 거 넣어주면됨,
{
for (A = 0; A < Size; A++) // A집합 도시의 개수가 K개여야함. A집합에서 1의 개수가 도시의 개수이다.
{
if (Count(A) != k) //A집합에 도시의 개수가 k개가 아니라면 넘겨줌.
continue;
for (int i = 2; i <= n; i++)
{
if (isIn(i, A)) //만약 A가 i에 있다면 진행x
continue; // i가 출발점임.
D[i][A] = minimum(n, i, j, A); //j를 먼저 밟을 때 최적의 경로가 나옴.
if (D[i][A] != INF)
Cnt++;
P[i][A] = j; // D[i][A]에서 i가 가장 먼저 밟는 도시가 j이다. //j를 밟을때 최적의 경로라른 뜻임.
}
}
}
A = Size - 1; //만약 도시의 개수가 3개라면 A집합은 (111)이다. 즉 2^(n-1) -1이다.
D[1][A] = minimum(n - 1, 1, j, A);
P[1][A] = j;
minlength = D[1][A];
Cnt++;
}전체 코드
/*
DP를 사용해서 Sales person 문제 풀기
D라는 2차원 배열을 만들고 D[i][j]는 i->1을 가는데 j를거치는 최단 경로의 길이라고 한다.
D[vi][A]를 에서 A를 집합형태로 만들어서 A집합에서 가장 최단경로를 구함.
W배열은 각각의 정점에서 다른 정점으로 가는 경로의 길이. 없을 시 INF로 무한대를 나타냄.
만약 A가 공집합이라면 그냥 그 정점에서 1까지 가는 경로를 구하면됨.
D[vi][A]=W[i][j]+D[vj][A-{vj}]를 j가 증가시켜주면됨. 이때 j는 A에속해야한다.
*/
#include <iostream>
#include <vector>
#include <algorithm>
#include <cmath>
using namespace std;
#define INF 999
int n, m, minl = 0, Size, Cnt = 0;
vector<vector<int>> D, W, P;
vector<int> path;
int Count(int A);
void travel(int n, vector<vector<int>> &P, int &minlength);
bool isIn(int i, int A);
int minimum(int n, int i, int &minJ, int A);
int diff(int A, int j);
void tour(int v, int A, vector<vector<int>> &P);
int main()
{
int cnt = 0;
cin >> n >> m;
D.resize(n + 1, vector<int>(pow(2, n - 1), 999));
W.resize(n + 1, vector<int>(n + 1, INF));
P.resize(n + 1, vector<int>(pow(2, n - 1), -1));
for (int i = 0; i < m; i++)
{
int s, f, l;
cin >> s >> f >> l;
W[s][f] = l;
}
for (int i = 1; i <= n; i++)
{
W[i][i] = 0; //인접행렬이므로 자신에서 자신으로 가는 경로는 0으로 초기화
}
travel(n, P, minl);
cout << minl << endl;
cout << 1 << " ";
tour(1, pow(2, n - 1) - 1, P); // 모든 도시를 포함하는 A값은 2^(N-1)-1이다. 예를 들어 n이 4일때 111이므로 7이다.
for (int i = 0; i < path.size(); i++)
{
if (i < path.size() - 1)
cout << path[i] << " ";
else
cout << path[i];
}
cout << endl;
for (int i = 1; i <= n; i++) // Cnt는 D배열에서 INF값이 아닌 것들의 수
{
for (int j = 0; j < pow(2, n - 1); j++)
{
if (D[i][j] != 999)
{
cnt++; //Cnt가 D[i][j]가 999가 아닌 갯수
if (cnt < Cnt)
cout << i << " " << j << " " << D[i][j] << endl;
else
cout << i << " " << j << " " << D[i][j];
}
}
}
}
void travel(int n, vector<vector<int>> &P, int &minlength)
{
int A, j, i; // A의 집합을 표현할려면 2진수 개념을 사용
//부분집합의 개수는 2^N-1개이다. N-1인 이유는 v1은 집합에 포함 안하기때문이다.
int Size = pow(2, n - 1);
for (i = 2; i <= n; i++)
{
D[i][0] = W[i][1]; //바로 가는 경로
if (D[i][0] != INF)
Cnt++;
}
for (int k = 1; k <= n - 2; k++)
// k는 내가 방문하고자 하는 도시의 개수. 총 n-2개의 도시를 방문해서 구하고 마지막 도시는 나중에 추가해줌.
//만약 n-1개를 방문했다면 그건 종결을 뜻함. n-2개 구하고 A집합에서 남은 거 넣어주면됨,
{
for (A = 0; A < Size; A++) // A집합 도시의 개수가 K개여야함. A집합에서 1의 개수가 도시의 개수이다.
{
if (Count(A) != k) //A집합에 도시의 개수가 k개가 아니라면 넘겨줌.
continue;
for (int i = 2; i <= n; i++)
{
if (isIn(i, A)) //만약 A가 i에 있다면 진행x
continue; // i가 출발점임.
D[i][A] = minimum(n, i, j, A); //j를 먼저 밟을 때 최적의 경로가 나옴.
if (D[i][A] != INF)
Cnt++;
P[i][A] = j; // D[i][A]에서 i가 가장 먼저 밟는 도시가 j이다. //j를 밟을때 최적의 경로라른 뜻임.
}
}
}
A = Size - 1; //만약 도시의 개수가 3개라면 A집합은 (111)이다. 즉 2^(n-1) -1이다.
D[1][A] = minimum(n - 1, 1, j, A);
P[1][A] = j;
minlength = D[1][A];
Cnt++;
}
int Count(int A) //A집합에 도시가 몇개 있는지 카운트함. A집합에서 1의 개수가 도시의 개수를 뜻함.
{
int cnt = 0;
for (; A != 0; A >>= 1) // A>>1은 A를 한칸씩 오른쪽으로 옮겨줌.
{
if (A & 1)
cnt++;
}
return cnt;
}
bool isIn(int i, int A)
//A집합에 i가 있는지 체크를 함. 있다면 true, 없다면 false를 리턴. v2부터 시작하므로 i-2자리만큼 왼쪽으로 이동시켜줘야함.
//예를 들어 2는 001, 3은 010, 4는 100 --> 001을 2는 0칸 3은 1칸 4는 2칸 왼쪽으로 이동시켜야 하므로 i-2만큼 왼쪽으로 이동시켜준다.
{
return (A & (1 << (i - 2))) != 0; // 1의 비트를 왼쪽으로 i-2만큼 이동시킴.
}
int minimum(int n, int i, int &minJ, int A)
//최소경로 길이를 구하는 함수.
//나는 A집합에 있는 도시들중 하나를 선정해서 최소경로를 구하고싶다. 따라서 J가 A에 있어야한다.
{
int minV = INF, value;
for (int j = 2; j <= n; j++)
{
if (isIn(j, A)==0) //j가 A집합에 없다면 진행하면 안됨.
continue;
int value = W[i][j] + D[j][diff(A, j)];
if (minV > value)
{
minV = value;
minJ = j; //그떄의 최소값에 도시를 minj에 넣어줌.
}
}
return minV;
}
int diff(int A, int j) //A집합에서 j에 해당하는 도시를 빼주는 함수.
//예를 들어 A가 111이고 j가 010이라면 j만 빼주는 방법은 j를 101(not계산)해서 A와 j를 and연산하면 된다.
{
return (A & ~(1 << (j - 2))); // 0과 1을 바꿈.
}
void tour(int v, int A, vector<vector<int>> &P) //경로를 구하는 함수.
//P[i][j]는 i->j까지 가는 경로에서 i가 첫번째로 밟는 도시이다.
//그럼 내가 출발점에서 모든 도시를 거쳐서 가는 경로중에서 첫번째가 k에 들어가고
//그 k를 출발점으로 선정후 k를 방문했으니 A집합에서 k를 빼줌.
//위 과정 반복
//만약 A가 0이라면 모든 도시를 방문했다는 뜻이니까 출발점으로 되돌아가야하기때문에 경로에 1을 추가해줌.
{
int k = P[v][A];
if (A == 0) //맨마지막에 경로는 1이여야함.
path.push_back(1);
else
{
path.push_back(k);
tour(k, diff(A, k), P);
}
}느낀 점
TSP의 개념은 해밀턴 회로와 비슷해서 쉬웠지만 이 문제를 DP로 풀려니까 엄청 어려웠고, A집합을 비트 연산자로 표현하고 A집합 관련 함수를 모두 비트연산자 관련으로 구현되어있어서 이해하기 힘들었다.