[알고리즘-C++] 분기한정(Branch & Bound)를 이용한 0-1 배낭 채우기

Skils/Algorithm

[알고리즘-C++] 분기한정(Branch & Bound)를 이용한 0-1 배낭 채우기

재한 2022. 5. 28. 23:11

되추적 알고리즘을 이용한 0-1 배낭 채우기를 앞에서 해보았다.

이번에는 분기한정을 이용한 0-1 배낭 채우기를 해보겠다. 되추적 알고리즘과 어떤 차이가 있는지를 중점으로 보면 될 것이다.

-앞선 문제와 동일하게

n= 보석의 개수

W= 배낭의 용량

n=4, W=13

p(profit)=[40,30,50,10], w(weight)=[2,5,10,5], p/w(단위 무게별 이익)=[20,6,5,2]

1. 앞선 0-1 배낭 채우기 문제와 같이 무게별 이익이 큰 순서대로 재 정렬한다.

2. 되추적 알고리즘과 상태 공간 트리를 구성한다.

3. 트리는 (profit, totweight, bound)로 이루어진다.

profit은 내가 가방에 담은 이익
totweight은 내가 가방에 담은 무게
bound는 내가 탐색한 부분에서 최대로 담을 수 있는 한계값

4. 가지치기 조건은 되추적 알고리즘과 동일하다.

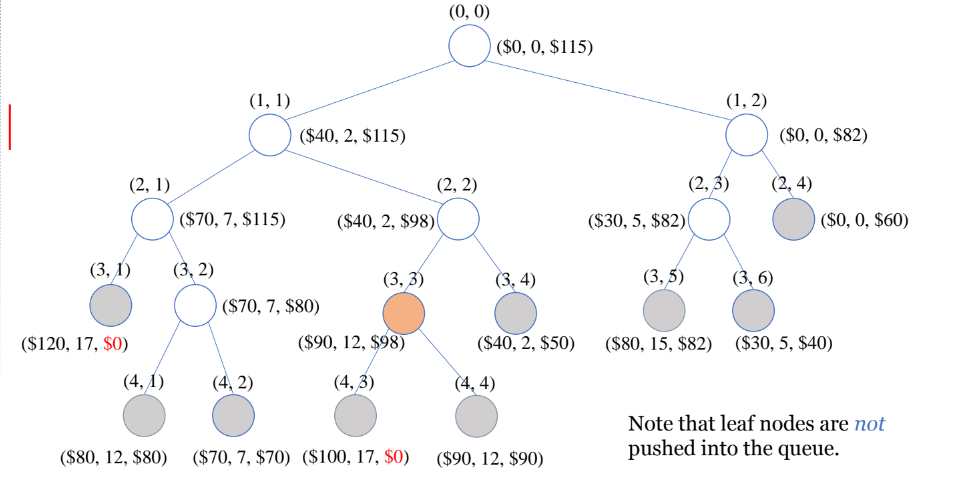
※되추적 알고리즘과 다른 점

(1,1)과 (1,2)를 비교해서 bound값이 가장 크면서 유망하고, 확장하지 않은 마디인 (1,1)의 자식들을 탐색한다.
(2,1), (2,2) 중에서 유망하고 확장하지 않은 마디인 (2,1)를 방문
(3,1)은 가지치기 조건에 의해서 방문 x (3,2)를 방문함.
(2,2)와 (3,2) 중에서 유망하고 확장하지 않은 마디인 (2,2)를 방문함.
(3,3)를 방문. 가지치기 조건에 걸리지 않아서 방문함.
(3,4)를 방문하는데 이미 (3,3)에서 maxprofit이 90으로 초기화되어서 (3,4)의 bound값이 maxprofit보다 작기 때문에 방문 x
(3,3)을 방문함.
(4,1)은 무게가 17, W를 넘기 때문에 방문 x
(4,2)는 한계값이 maxprofit보다 같기 때문에 유망하지 않다고 결정, 그 뒤에 자식 노드들은 이미 maxprofit을 넘을 수 없는 구조기 때문에 확장을 하지 않는다.

--> 결과 (3,3)이 가장 유망한 방문이다.

구현

1. 구조체 선언

typedef struct node *node_p;
typedef struct node
{
    int level;
    int weight;
    int profit;
    float bound;
} nodetype;

2. 우선순위 대기열(priority queue)을 사용한다.

정렬 조건은 bound값이 큰 순서대로 넣어준다.
이유는 bound값이 가장 큰 게 유망하기 때문에 그 유망한 노드를 찾기 위해서 pq.top을 사용해야 함.

3. Bound계산

bound값은 내가 현 상황에서 가장 큰 이익을 계산해줌.(실제로는 보석을 분할할수는 없지만 분할할수있다고 가정하고 계산)

float bound(node_p u)
{
    int j, k, totweight;
    float result;
    if (u->weight >= W) //그때 방문했던 노드의 무게 합이 W보다 크다면 잘못된 방문임을 뜻함.
        return 0;
    else
    {
        result = u->profit;
        j = u->level + 1;
        totweight = u->weight;
        while (j <= N && totweight + Weight[j] <= W)
        {
            totweight += Weight[j];
            result += profit[j];
            j++;
        }
        k = j;
        if (k <= N)
            result += (W - totweight) * ((float)profit[k] / Weight[k]);
        return result;
    }
}

4. 배낭 채우기 함수

void knapsack6()
{
    priority_queue<node_p, vector<node_p>, compare> pq; // bound값으로 내림차순 정렬해서 넣어줫음.
    node_p u, v;
    u = (node_p)malloc(sizeof(nodetype) * N);
    v = (node_p)malloc(sizeof(nodetype) * N);
    maxprofit = 0;
    v = create_node();
    v->level = 0;
    v->profit = 0;
    v->weight = 0;
    v->bound = bound(v);
    print_node(v);
    pq.push(v);
    while (!pq.empty())
    {
        v = pq.top();
        pq.pop();
        // print_node(v);
        if (v->bound > maxprofit)
        {
            //가방에 보석을 담은경우
            u = create_node();
            u->level = v->level + 1;
            u->weight = v->weight + Weight[v->level + 1];
            u->profit = v->profit + profit[v->level + 1];
            u->bound = bound(u);
            print_node(u);
            if (u->weight <= W && u->profit > maxprofit) //내가 다음 노드로 진행햇는데 그때의 무게가 W보다 작거나 같아야함.
            {
                maxprofit = u->profit; //그때의 이익이 만약 maxprofit보다 크다면 최신화시켜줌.
            }
            if (u->bound > maxprofit)
            {
                pq.push(u); //내가 설정한 바운드값보다 maxprofit이 크다면 pq에 푸쉬해줌.
            }
            //가방에 보석을 담지 않는 경우.
            u = create_node();
            u->level = v->level + 1;
            u->weight = v->weight;
            u->profit = v->profit;
            u->bound = bound(u);
            print_node(u);
            if (u->bound > maxprofit)
            {
                pq.push(u);
            }
        }
    }
}

코드

/*
branch&Bound를 이용한 0-1 Knapsack problem
무게대비 이득을 내림차순으로 정렬
유망한것부터 탐색함.
유망한것은? Bound값이 높은것.
Prority queue를 이용함. Bound값을 기준으로 내림차순 정렬
내가 탐색한 노드의 바운드 값이 maprofit보다 낮다면 굳이 탐색할 필요가없음.
*/
#include <iostream>
#include <vector>
#include <algorithm>
#include <queue>

using namespace std;
typedef struct node *node_p;
typedef struct node
{
    int level;
    int weight;
    int profit;
    float bound;
} nodetype;
struct compare
{
    bool operator()(node_p a, node_p b)
    {
        return a->bound < b->bound;
    }
};
int N, W;
vector<int> profit;
vector<int> Weight;
int maxprofit;
void knapsack6();
float bound(node_p u);
node_p create_node();
void print_node(node_p u);
int main()
{
    cin >> N >> W;
    Weight.resize(N + 1);
    profit.resize(N + 1);
    for (int i = 1; i <= N; i++)
    {
        int w;
        cin >> w;
        Weight[i] = w;
    }
    for (int j = 1; j <= N; j++)
    {
        int a;
        cin >> a;
        profit[j] = a;
    }
    // profit/weight 큰 것으로 정렬
    for (int i = 1; i <= N; i++)
    {
        for (int j = i + 1; j <= N; j++)
        {
            if (profit[i] / Weight[i] < profit[j] / Weight[j]) // 앞에게 더 크다면 나둠
            {
                swap(profit[i], profit[j]);
                swap(Weight[i], Weight[j]);
            }
        }
    }
    knapsack6();
    cout << maxprofit;
}
void knapsack6()
{
    priority_queue<node_p, vector<node_p>, compare> pq; // bound값으로 내림차순 정렬해서 넣어줫음.
    node_p u, v;
    u = (node_p)malloc(sizeof(nodetype) * N);
    v = (node_p)malloc(sizeof(nodetype) * N);
    maxprofit = 0;
    v = create_node(); //v는 초기 root node임.
    v->level = 0;
    v->profit = 0;
    v->weight = 0;
    v->bound = bound(v);
    print_node(v);
    pq.push(v);
    while (!pq.empty())
    {
        v = pq.top();
        pq.pop();
        // print_node(v);
        //bound는 이익의 상한선.
        if (v->bound > maxprofit) //만약 bound가 maxprofit보다 작다면 밑에 것은 굳이 탐색할 필요가 없음,.
        {
            //가방에 보석을 담은경우
            u = create_node();
            u->level = v->level + 1;
            u->weight = v->weight + Weight[v->level + 1];
            u->profit = v->profit + profit[v->level + 1];
            u->bound = bound(u);
            print_node(u);
             //보석을 담았는제 가방 무게인 W를 초과해선 안되고 담은 이익이 maxprofit 보다 크다면 초기화시켜줌.
            if (u->weight <= W && u->profit > maxprofit)
            {
                maxprofit = u->profit; 
            }
            if (u->bound > maxprofit) //bound값이 maxprofit보다 작다면 유망하지않음. 
            {
                pq.push(u); 
            }

            //가방에 보석을 담지 않는 경우.
            u = create_node();
            u->level = v->level + 1;
            u->weight = v->weight;
            u->profit = v->profit;
            u->bound = bound(u);
            print_node(u);
            if (u->bound > maxprofit) // bound값이 maxprofit보다 작다면 유망하지않음. 
            {
                pq.push(u);
            }
        }
    }
}
node_p create_node()
{
    node_p temp;
    temp = (node_p)malloc(sizeof(nodetype) * N);
    return temp;
}
float bound(node_p u)
{
    int j, k, totweight;
    float result;
    if (u->weight >= W) //그때 방문했던 노드의 무게 합이 W보다 크다면 잘못된 방문임을 뜻함.
        return 0;
    else
    {
        result = u->profit;
        j = u->level + 1;
        totweight = u->weight; //현재무게
        while (j <= N && totweight + Weight[j] <= W) //보석의 끝까지 탐색하며 현재무게가 제한무게가 될때까지 더해줌.
        {
            totweight += Weight[j];
            result += profit[j];
            j++;
        }
        k = j;
        if (k <= N) //만약 무게를 초과햇는데 가방을 끝까지 돌지못했다면 쪼개서 넣어줌.
            result += (W - totweight) * ((float)profit[k] / Weight[k]);
        return result;
    }
}
void print_node(node_p u)
{
    cout << u->level << " " << u->weight << " " << u->profit << " " << u->bound << endl;
}

💡정리

bound와 totweight의 개념을 잘 이해해야함.
- bound는 내가 기대할수있는 이익의 상한선. 이것보다 더 큰 이익은 그 경로에서 나올수가없다.
  - bound는 내가 현재 담을 수 있는 최대의 이익을 구하면 됨.(분할가능)
  - 따라서 bound값이 maxprofit보다 작거나 같다면 유망하지 않으므로 탐색x
- totweight는 현재 내가 담은 무게.
  - W보다 작거나 같아야함.
node 탐색 순서는 BFS를 따르지만 BFS + Branch & Bound를 이용함.
- 여기서 탐색 우선순위는 Bound값이 높은 노드다.
- 당연히 Bound값이 높은 노드들에서 최적값을 찾을 확률이 높다.

느낀 점

배낭 문제를 워낙 많이 풀다 보니까 분기 한정이라는 새로운 기법(?)으로 풀어도 이해하기 쉬웠다.
분기 한정과 되추적 알고리즘의 디테일한 차이를 아는 것이 이번 단원의 중요한 목표인 것 같다.

저작자표시