[C++]알고리즘 - 기사의 여행 문제와 해밀턴 경로

Skils/Algorithm

[C++]알고리즘 - 기사의 여행 문제와 해밀턴 경로

재한 2022. 5. 28. 01:37

문제

n * m 체스보드에서 기사의 여행 문제를 해결하는 백트래킹 알고리즘을 구현하시오.
Knight's Tour 문제는 해밀턴 경로(path)와 해밀턴 회로(circuit, cycle)를 찾는 문제로 구분할 수 있다.
해밀턴 회로는 출발 정점과 무관하게 회로의 수를 구할 수 있고,
해밀턴 경로는 출발 정점에 따라 가능한 경로의 수가 달라짐에 유의하시오.

입력

첫 번째 줄에 체스보드의 크기 n(행의 크기)과 m(열의 크기)이 주어진다.
두 번째 줄에 출발 정점의 개수 T가 주어진다.
이후로 T개의 출발정점이 i(row), j(col)의 쌍으로 주어진다.

출력

첫 번째 줄에 해밀턴 회로의 개수를 출력한다.
두 번째 줄부터 입력에서 주어진 출발정점 각각에 대해 해밀턴 경로의 수를 한 줄에 하나씩 출력한다.

문제 해석

해미털 회로와 경로의 차이를 알아야 한다.
1. 해밀턴 회로란 출발 정점에서 모든 정점을 각 한 번씩 방문하고 다시 출발 정점으로 돌아와야 한다.
2. 해밀턴 경로란 출발 정점에서 모든 정점을 각 한 번씩 방문하기만 하면 된다. (다시 출발점으로 돌아올 필요가 없음.)
knight의 이동반경을 알아야 한다.
1. 문제에서 knight는 체스에서 knight를 의미하며 kngiht가 갈 수 있는 방향은 아래 그림과 같다.
2. 자기 자신을 기준으로 8방향을 갈 수 있다.

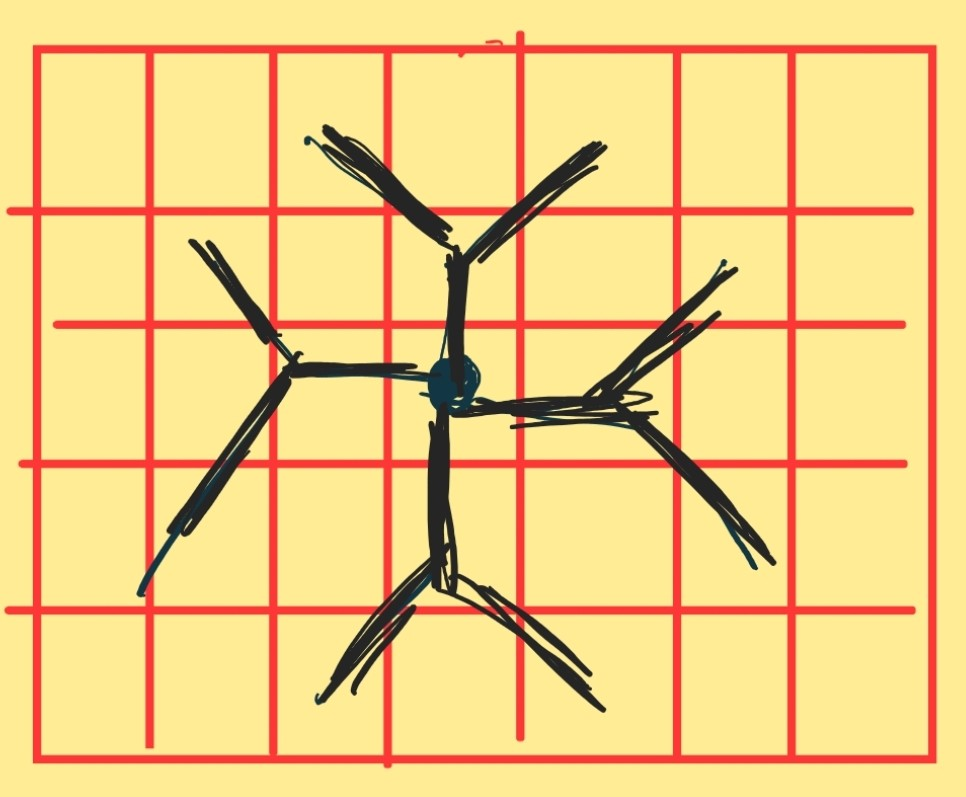
3. n*m 체스판을 행렬로 만들면 n, m의 값이 커지면 시간이 오래 걸림

--> 자료구조를 행렬이 아닌 인접 리스트를 선택.

grpah [n][m] 배열이 아닌 size가 n*m인 일차원 배열을 만들어준다.

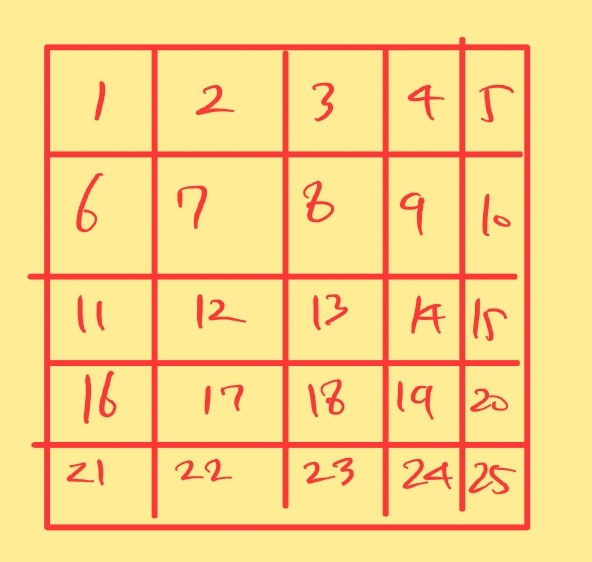
1차원 vector visit를 만들어주고 visit의 size는 n*m+1이 될 것이다. 1~25까지 있어야 하기 때문이다.
만약 n번지를 방문했다면 visit [n]=1로 초기화해준다.
각 위치마다 나이트의 이동 법칙에 의해서 갈 수 있는 경로가 있다.
location 1 : [8,12], location 2 : [11,9,13] 등등이 있을 것이다. 그때의 location을 i로 , j를 갈 수 있는 위치로 가정하고
graph [i][j]를 1로 초기화시켜준다. graph값이 1이라는 뜻은 갈 수 있는 경로라는 뜻이다.
예를 들어 graph [1][8]은 1에서 8까지 갈 수 있으므로 값은 1이 된다. 하지만 graph [1][7]은 경로가 없으므로 0이다.

4. 가지치기 조건을 이용해서 재귀 함수를 사용, 결과를 도출.

만약 경로가 없는 곳이라면? 방문 x
경로가 있더라도, 이미 방문한 곳을 또 방문할 예정이라면, 그 방문은 불필요하기 때문에 탐색 x
만약 마지막 노드를 방문했는데, 그 마지막 노드와 출발점이 연결이 안 되어있다면, 회로 추가 x
마지막 노드를 방문할 차례고, 지금 방문하려는 노드와 직전에 방문한 노드가 경로가 있고, 각 한 번씩 방문한 노드라면, 경로 추가

구현

1. 해당되는 나이트의 경로마다 연결해주기

void Move(int i)
{
	int row = i / m;
	int col = i % m;
	if (row - 2 >= 0 && col - 1 >= 0)
	{

		graph[i][(row - 2) * m + col - 1] = 1;
		graph[(row - 2) * m + col - 1][i] = 1;
	}
	if (row - 2 >= 0 && col + 1 <= m - 1)
	{
		graph[i][(row - 2) * m + col + 1] = 1;
		graph[(row - 2) * m + col + 1][i] = 1;
	}
	if (row + 2 <= n - 1 && col + 1 <= m - 1)
	{
		graph[i][(row + 2) * m + col + 1] = 1;
		graph[(row + 2) * m + col + 1][i] = 1;
	}
	if (row + 2 <= n - 1 && col - 1 >= 0)
	{
		graph[i][(row + 2) * m + col - 1] = 1;
		graph[(row + 2) * m + col - 1][i] = 1;
	}
	if (row + 1 <= n - 1 && col - 2 >= 0)
	{
		graph[i][(row + 1) * m + col - 2] = 1;
		graph[(row + 1) * m + col - 2][i] = 1;
	}
	if (row + 1 <= n - 1 && col + 2 <= m - 1)
	{
		graph[i][(row + 1) * m + col + 2] = 1;
		graph[(row + 1) * m + col + 2][i] = 1;
	}
	if (row - 1 >= 0 && col + 2 <= m - 1)
	{
		graph[i][(row - 1) * m + col + 2] = 1;
		graph[(row - 1) * m + col + 2][i] = 1;
	}
	if (row - 1 >= 0 && col - 2 >= 0)
	{
		graph[i][(row - 1) * m + col - 2] = 1;
		graph[(row - 1) * m + col - 2][i] = 1;
	}
}

-> 각 출발지마다 갈 수 있는 경로는 1로 초기화된다.

2. 가지치기 함수

bool promising(int i, int node, int start) //방문한곳이면 안간다. 그리고 갈 수있는 곳은 미리 체크하는게 나을까? 경로가 없으면 0 경로가 있으면 1이다. node가 내가 갈곳 start는 내가있는곳
{
	//마지막 정점일때는 거기서 출발점까지의 경로가 무조건 있어야함.
	bool flag = true;
	bool opt;
	int now = 0;
	if (i == Size && graph[visit[Size]][start] != 1) //회로는 출발점을 다시 돌아와야함. //visit[Size]가 맨 마지막에 방문한 노드일거다 아마.
	{
		flag = false;
	}
	if (i == Size && graph[visit[i]][visit[i - 1]] == 1) //경로는 출발점을 다시 안와도됨. //이미 방문한 노드여도 cnt가 ++됨.
	{
		opt = true;					//초기는 하고 만약에 같은게 없다면 flag는 true이므로
		for (int k = 0; k < i; k++) // Size를 i보다 작을때로 바꿈 자기자신은 검사할필요가없네
		{
			// cout << visit[k] << " ";
			if (visit[i] == visit[k]) //이미 방문한 곳이라면
			{
				opt = false;
				flag = false;
			}
		} //반복문이 안걸리고 나오면 트루라는뜻
		if (opt == true)
		{
			Cnt++;
		}
	}
	else if (i > 0 && graph[visit[i]][visit[i - 1]] != 1) //연결안되어있는건 걍 재낌.
	{
		flag = false;
	}
	else //연결되어있다면 방문했는지 안했는지 체크를 해야함.
	{
		flag = true;
		while (now < i)
		{
			if (visit[now] == visit[i])
			{
				flag = false;
			}
			now++;
		}
	}
	return flag;
}

3. 모든 노드를 방문하는 함수(적절한 가지치기를 통해서 불필요한 탐색 x)

void knight(int i, int node, int start, int now)
{
	bool opt = true;
	if (promising(i, node, start)) // node는 내가 가려는 곳 start는 출발 정점.
	{
		if (i == n * m - 1)
		{
			cnt++;
		}
		else
		{
			for (int j = 0; j <= Size; j++)
			{
				// visit[i]기준으로 갈 수 있는 방향을 선정해야함.

				if (graph[visit[i]][j] == 1) //경로가 있고
				{
					visit[i + 1] = j;
					knight(i + 1, j, start, visit[i]); // knight탈출하면 방문안햇다는 뜻임.
					visit[i + 1] = 0;
				}
			}
		}
	}
}

전체 코드

/*
1.해밀턴의 회로의 수는 어디서 출발하든 같다.
2.해밀턴 회로란 출발점에서 모든 노드를 방문하고 마지막에 다시 출발점으로 오는 경로의수다. 여기서 주의할점은 모든 노드를 딱 한번만 방문해야한다는점이다.
3.하지만 해밀턴 경로의 수는 출발정점에 따라 다르다.
4.정점의 수는 n*m이다. 종료 조건은 i가 n*m이 될떄이면 될것이다.
5.kngiht가 이동할 수 있는 방향은 8가지이다.
6.나이트가 정점마다 갈 수있는 경로를 뽑는게 좋을거같은데
7.체스판을 0번부터 n*m-1번까지 1차원 배열로 만든다.
8.각 정점마다 갈 수 있는 수는
*/
//해밀턴회로만 신경쓰자.
#include <iostream>
#include <vector>
#include <algorithm>
#include <map>
using namespace std;
int n, m, T, cnt = 0, Cnt;
vector<int> visit;
int Size;
vector<vector<int>> graph;
void Move(int i);
void knight(int i, int node, int start, int now);
bool promising(int i, int node, int first);
int main()
{
	cin >> n >> m; // n은 row, m은 col
	Size = n * m - 1;
	visit.resize(n * m);
	// Visit.resize(n * m);
	graph.resize(n * m, vector<int>(m * n, 0));
	for (int i = 0; i <= Size; i++)
	{
		Move(i); //
	}
	knight(0, 0, 0, 0);
	visit.resize(n * m, 0);
	cout << cnt << endl;
	Cnt = 0;
	cin >> T;
	for (int i = 0; i < T; i++)
	{
		int s, f;
		cin >> s >> f;
		int vv = s * m + f;
		visit[0] = vv;
		knight(0, 0, vv, 0); // i,node,start,now
		if (i < T - 1)
		{
			cout << Cnt << endl;
		}
		else
			cout << Cnt;
		Cnt = 0;
	}
}
void knight(int i, int node, int start, int now)
{
	bool opt = true;
	if (promising(i, node, start)) // node는 내가 가려는 곳 start는 출발 정점.
	{
		if (i == n * m - 1)
		{
			cnt++;
		}
		else
		{
			for (int j = 0; j <= Size; j++)
			{
				// visit[i]기준으로 갈 수 있는 방향을 선정해야함.

				if (graph[visit[i]][j] == 1) //경로가 있고
				{
					visit[i + 1] = j;
					knight(i + 1, j, start, visit[i]); // knight탈출하면 방문안햇다는 뜻임.
					visit[i + 1] = 0;
				}
			}
		}
	}
}
bool promising(int i, int node, int start) //방문한곳이면 안간다. 그리고 갈 수있는 곳은 미리 체크하는게 나을까? 경로가 없으면 0 경로가 있으면 1이다. node가 내가 갈곳 start는 내가있는곳
{
	//마지막 정점일때는 거기서 출발점까지의 경로가 무조건 있어야함.
	bool flag = true;
	bool opt;
	int now = 0;
	if (i == Size && graph[visit[Size]][start] != 1) //회로는 출발점을 다시 돌아와야함. //visit[Size]가 맨 마지막에 방문한 노드일거다 아마.
	{
		flag = false;
	}
	if (i == Size && graph[visit[i]][visit[i - 1]] == 1) //경로는 출발점을 다시 안와도됨. //이미 방문한 노드여도 cnt가 ++됨.
	{
		opt = true;					//초기는 하고 만약에 같은게 없다면 flag는 true이므로
		for (int k = 0; k < i; k++) // Size를 i보다 작을때로 바꿈 자기자신은 검사할필요가없네
		{
			// cout << visit[k] << " ";
			if (visit[i] == visit[k]) //이미 방문한 곳이라면
			{
				opt = false;
				flag = false;
			}
		} //반복문이 안걸리고 나오면 트루라는뜻
		if (opt == true)
		{
			Cnt++;
		}
	}
	else if (i > 0 && graph[visit[i]][visit[i - 1]] != 1) //연결안되어있는건 걍 재낌.
	{
		flag = false;
	}
	else //연결되어있다면 방문했는지 안했는지 체크를 해야함.
	{
		flag = true;
		while (now < i)
		{
			if (visit[now] == visit[i])
			{
				flag = false;
			}
			now++;
		}
	}
	return flag;
}
void Move(int i)
{
	int row = i / m;
	int col = i % m;
	if (row - 2 >= 0 && col - 1 >= 0)
	{

		graph[i][(row - 2) * m + col - 1] = 1;
		graph[(row - 2) * m + col - 1][i] = 1;
	}
	if (row - 2 >= 0 && col + 1 <= m - 1)
	{
		graph[i][(row - 2) * m + col + 1] = 1;
		graph[(row - 2) * m + col + 1][i] = 1;
	}
	if (row + 2 <= n - 1 && col + 1 <= m - 1)
	{
		graph[i][(row + 2) * m + col + 1] = 1;
		graph[(row + 2) * m + col + 1][i] = 1;
	}
	if (row + 2 <= n - 1 && col - 1 >= 0)
	{
		graph[i][(row + 2) * m + col - 1] = 1;
		graph[(row + 2) * m + col - 1][i] = 1;
	}
	if (row + 1 <= n - 1 && col - 2 >= 0)
	{
		graph[i][(row + 1) * m + col - 2] = 1;
		graph[(row + 1) * m + col - 2][i] = 1;
	}
	if (row + 1 <= n - 1 && col + 2 <= m - 1)
	{
		graph[i][(row + 1) * m + col + 2] = 1;
		graph[(row + 1) * m + col + 2][i] = 1;
	}
	if (row - 1 >= 0 && col + 2 <= m - 1)
	{
		graph[i][(row - 1) * m + col + 2] = 1;
		graph[(row - 1) * m + col + 2][i] = 1;
	}
	if (row - 1 >= 0 && col - 2 >= 0)
	{
		graph[i][(row - 1) * m + col - 2] = 1;
		graph[(row - 1) * m + col - 2][i] = 1;
	}
}

느낀 점 :

너무 불필요하게 길게 짠 것 같다. backtracking에서 가지치기를 효율적으로 짜야 알고리즘의 효율성이 높아지는데 내가 짠 가지치기의 조건과 방법이 조금 너무 노가다(?)가 아니었나 싶다.. ㅎ,, 다른 사람 코드를 보고 많이 반성했다.

저작자표시